Ejuh_62

The African Review of Physics (2013) 8:0062 463
Linear and Non Linear Optical Effects of Pyrimethamine and Sulfadoxine:
Ab-initio and Density Functional Study
Geh Wilson Ejuh1, 2,* and Ndjaka Jean Marie1 1University of Dschang, IUT Bandjoun, Department of General and Scientific Studies, Bandjoun, Cameroon 2Université de Yaoundé I, Faculté des Sciences, Département de Physique, Yaounde, Cameroun The molecular structures of pyrimethamine and sulfadoxine have been explored for non linear optical effects. The ab- initio Hartee Fock calculations and Density Functional Theory with B3LYP method have been carried out employing 6-311++G** basis set. The dipole moments (µ), polarizability (α), and first hyperpolarizability (βmol) in gas phase and in solvated medium (water and ethanol) are calculated using the same level of theory. The variation of the C-N bond lengths suggests that there is an extended pi-electron delocalization over the pyrimidine moiety that is responsible for non linearity of these molecules. Equally, the large values of βmol for these molecules suggest potential applications of these molecular systems in the development of non linear materials. The large βmol values, which is a measure of the non linear optical activity of the molecular system, is associated with the intermolecular charge transfer resulting from an electron cloud movement through the pi-electron delocalization. Hence theoretical determination of βmol is quite useful, both in the understanding of relationship between the molecular structure and non linear optical properties. 1. Introduction
molecular systems have been studied for predicting nonlinearity [12]. Organic compounds with Molecular materials with non linear optical (NLO) electron donating group on one side of the properties are currently attracting considerable molecule and electron accepting group on other attention because of their potentials applications in side have been studied by experimental and optoelectronics devices used in telecommunication, theoretical scientists for NLO properties [13]. information storage, optical switching, signal Designs of these organic NLO active materials are processing, and terahertz wave generation [1,2,3,4]. based on the approach of charge transfer due to π- Non linear optics is one of the few research electron cloud movement from donor to acceptor frontiers where tremendous interest arises not only groups on either side of these π-conjugated from the desire to understand new physical systems. This in turn affects the value of phenomena but also from the potential of polarizability and hyper-polarizability [7]. It has technology applications [5]. been known from recent studies that molecular Organic molecules with delocalized π-electrons systems, based on electron donor and electron showing large values of non linear optical acceptor units connected through pi electron parameters are gaining interest among researcher moieties, show many interesting non-linear optical because of their potential applications in the field characteristics and have higher value of second of optoelectronics, such as optical communication, order NLO properties [14,15,16,17]. The types of optical computing, optical switching, and image pi-bridges studied so far for developing efficient processing [6,7,8,9,10]. The electro-optic effect NLO materials and molecules include donor- arises in photorefractive materials (optoelectronic acceptor acetylenes [18], azo complexes [19], materials) in two forms; linear electro-optic (LEO) aromatic ring [14] and hetero-aromatic rings [20]. effect or Pockels effect and quadratic electro-optic A good deal of work has been done for (QEO) effect or Kerr effect. Organic molecules are good materials for nonlinear devices as they are conjugated polymers consisting of six member and chemically flexible and show a large and fast non five-member aromatic units, such as benzene, linear optical response [11] as a result of which pyridine, Thiophene, pyrrole, N,N- dimethyl-5- their optical and electronic properties can be studied. A number of organic and organometallic 2-amine 5-nitro-2-phenylpyridine, and others [20,21]. Their derivatives are also considered to be *[email protected] promising materials for electronic and nonlinear The African Review of Physics (2013) 8:0062 464
optical technology. So far many studies have also initio and DFT calculations have been carried out been carried out to investigate the nonlinear with 6-311++G** basis set. behavior of two π-conjugated rings attached with a single bond such as biphenyls [20] and 2. Computational Methodology
phenylpyridine [22]. However, pyrimethamine and All calculations of polarizability and first static Sulfadoxine can further be investigated as a bridge hyper-polarizability for the search of better NLO materials and for an Sulfadoxine molecules were performed using understanding of the mechanism at atomic level. Gaussian 03W [28]. Initial geometry optimizations Theoretical calculations are quite useful both in were performed using the ab-initio RHF method understanding the relationship between molecular with 3-21G basis set. Subsequently, its results were structures and nonlinear optical properties, and also utilized to 6-31G basis set and final calculations provide guidelines to experimentalists for the were carried out with double polarized triple zeta design and synthesis of new organic NLO split valence 6-311++G** basis set. These materials. A large number of semi-empirical and ab structures were refined further using Density initio calculations have been reported on molecular Functional Theory, which is a cost effective hyperpolarizability (β), which is one of the key method for inclusion of electron correlations with parameter in the investigation of second order NLO the three-parameter density functional generally materials [23,24,25]. Experimental measurements known as Becke3LYP (B3LYP). This includes and theoretical calculations on molecular hyper- Becke's gradient exchange corrections [29], the polarizability have become one of the key factors Lee, Yang and Parr correlation functional [30] and in the determination of second-order NLO material the Vosko, Wilk and Nusair correlation functional design. Though, there is an effect of the basis set [31] with a 6-311++G** basis set. As the first step, to determine the value of first molecular hyper- geometry optimizations were carried out and then polarizability and electronic properties of the IR and Raman frequencies were calculated using molecule. The effect is not very high but the the Hessian, which is the matrix of second electronic properties and the hyper-polarizability derivatives of the energy with respect to the values have been reported to slightly increased on geometry. We have chosen 6-311++G** basis set, taking up higher basis sets like the 6-31G and 6- which has been supplemented by including diffuse 311++G** [18,26]. For this reason we have and polarization functions in order to ensure proper decided to carry out our computation using higher basis set. Equally, as documented in literature, polarizabilities. This basis set is an adequate basis accurate estimate of polarizability and hyper- set and allows for physically correct polarization of polarizability need polarized and diffused basis sets the molecule in the presence of an electric field. as well as introduction of electron correlation contributions [27]. properties requires the use of extended basis sets The aim of the present work is to predict NLO and a high level of theory [22], hence the used of properties of molecules Pyrimethamine and B3LYP in our calculations. sulfadoxine. The idea is to study the charge transfer The values of mean polarizability (α) of effect from donor to acceptor through Pyrimidine molecular systems and the isotropy (γ ) reported in moiety and determine theoretically the hyper-polarizability of these molecules. This is because the present work were calculated by using the following equations polarizability is quite useful to understand both the relationship between their molecular structure and their NLO properties. In calculating the non linear behavior for the designed molecular systems, ab- − yy )2 + ( yy − zz ) 2 + ( zz − xx ) + 6 xy + yz + The total hyper-polarizability is defined as

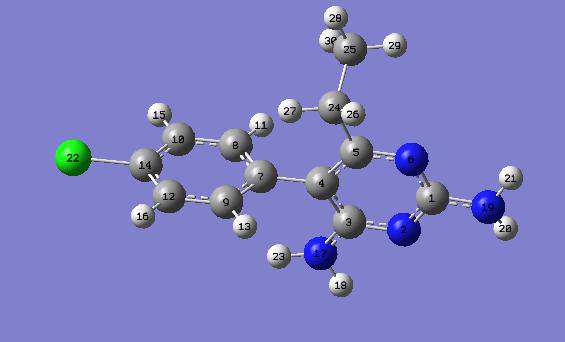
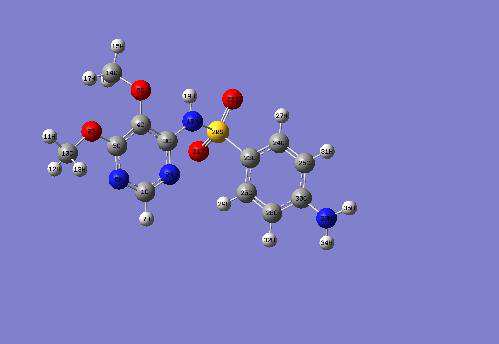
The African Review of Physics (2013) 8:0062 465
The magnitude of βmole is calculated from the computed components β using following equations ( ikk kik kki) 3 i,k k = x, y, z; i = x, y, z (4) Fig.2: Optimized structure of Sulfadoxine [26,33]. ([ xxx xyy xzz )2 3.1. Optimized geometrical properties of
The geometrical parameters of a Pyrimethamine molecule in gas phase, water and ethanol are listed in Tables 1a and 1b. The calculated bond lengths at 3. Molecular Structure and Geometrical
RHF/6-311++G** level are slightly smaller Properties
(ranging from 0.01Å to 0.04Å) than their corresponding values obtained at the B3LYP/6- The molecular structure of Pyrimethamine is 311++G** level (Table 1a). It seems that inclusion shown in Fig. 1 and that of Sulfadoxine is shown in of electrons correlation expand the molecules. Fig. 2. The geometric optimization of any system Once dissolved (in water and ethanol), the bond gives the ground state geometry of that system. The lengths remain unaffected at RHF/6-311++G** total ground state energy of a system is obtained as level while at B3LYP/6-311++G** level, the bond a function of the coordinates of the nuclei from lengths vary slightly except for the following N2- Born-Oppenheimer (BO) approximation. The C3, C5-N6, C5-C4, C7-C8, C7-C9, C9-C12, C12- ground state geometry corresponds to the minimum C14, C8-H11, C9-H13, C10-H15,C12-H16, C24- total ground state energy whereas a first order H27, C25-H28, C25-H29 and C25-H30, all of saddle point on the BO surface gives the transition which remain unaffected. The bond lengths (Table state geometry. Molecular geometries were fully 1a) at the RHF/6-311++G** and at the B3LYP/6- optimized using Berny's optimization algorithm in 311++G** are approximately equal to the Gaussian 03, as well as redundant internal experimental results [34,35,36]. The B3LYP/6- 311++G** results are in better accord with the experimental results and with the theoretical results given by [37]. For example in the Pyrimidine ring, the C5-N6 and C1-N6 bond lengths are exactly equal to those given by [37] and are 0.017Å and 0.013 Å smaller than the C-N experimental value, respectively, both in gas phase and in dissolved phase at the B3LYP/6-311++G** level. At the RHF/6-311++G** level, the C5-N6 and C1-N6 bond lengths are 0.029 Å and 0.041 Å smaller than the C-N experimental value, respectively, both in the gas phase, water and ethanol. From Table 1a, we observed that C-N bond lengths on the Pyrimidine ring vary slightly. This variation of Fig.1: Optimized Structure of Pyrimethamine [32,33]. the C-N bond lengths suggests that there is an extended pi-electron delocalization over the pyrimidine moiety. The bond angles vary from 0.1 to 0.2 degree(s) in both RHF and DFT levels of theories with the 6- The African Review of Physics (2013) 8:0062 466
311++G** basis set (Table 1b). The six member angles vary slightly as we move from gas phase to carbon ring (Phenyl) and the other ring with two of solution phase. Most of the bond angles increases the carbon atoms replaced by Nitrogen atoms as we move from gas medium to water and ethanol (pyrimidine) possibly give added stability to the with the increase more significant in ethanol. The molecule. The nitrogen atoms (N11, N12, N14 and bond angles (Table 1b) at the RHF/6-311++G** N17) play a major role in the electron density and at the B3LYP/6-311++G** are approximately configuration. Once dissolved (in water and equal to the experimental results [34,35,36]. The ethanol) the bond angles remain unaffected at RHF/6-311++G** results are in better accord with RHF/6-311++G** level of theory while at the experimental results. B3LYP/6-311++G** level of theory, the bond Table 1a: Optimized geometrical parameters – Bond lengths of Pyrimethamine molecule in different mediums obtained by RHF and B3LYP methods employing 6- 311++G** basis sets and their corresponding experimental values in gas. B3LYP/6-311++G** 1.3244 1.3395 1.3394 1.3394 1.3185 1.3372 1.3372 1.3371 R(C1- N19) 1.3582 1.3582 1.3691 1.3693 1.3693 1.3187 1.3344 1.3344 1.3344 R(C3-N17) 1.3547 1.3547 1.3678 1.3679 1.3680 1.3305 1.3429 1.3429 1.3429 1.4131 1.4199 1.4198 1.4199 1.3839 1.3974 1.3974 1.3974 1.4967 1.4922 1.4921 1.4921 R(C5-C24) 1.5101 1.5101 1.5113 1.5112 1.5111 1.3911 1.4019 1.4019 1.4019 1.402 1.3914 1.4020 1.4020 1.4020 1.402 R(C8-C10) 1.3853 1.3853 1.3933 1.3932 1.3932 R(C9-C12) 1.3854 1.3854 1.3933 1.3933 1.3933 R(C12-C14) 1.3812 1.3812 1.3909 1.3909 1.3909 R(C24-C25) 1.5329 1.5329 1.5383 1.5382 1.5382 R(C10-C14) 1.3813 1.3813 1.3910 1.3911 1.3911 R(C14-Cl22) 1.7450 1.7450 1.7594 1.7593 1.7593 R(C8-H11) 1.0752 1.0752 1.0843 1.0843 1.0843 1.082 R(C9-H13) 1.0756 1.0756 1.0844 1.0844 1.0844 R(C10-H15) 1.0737 1.0737 1.0827 1.0827 1.0827 R(C12-H16) 1.0737 1.0737 1.0827 1.0827 1.0827 R(C24-H26) 1.0849 1.0849 1.0939 1.0940 1.0940 R(C24-H27) 1.0821 1.0821 1.0910 1.0910 1.0910 R(C25-H28) 1.0858 1.0858 1.0932 1.0932 1.0932 R(C25-H29) 1.0836 1.0836 1.0917 1.0917 1.0917 R(C25-H30) 1.0863 1.0863 1.0937 1.0937 1.0937 R(N17-H18) 0.9929 0.9929 1.0076 1.0077 1.0077 R(N17-H23) 0.9914 0.9914 1.0064 1.0065 1.0065 The African Review of Physics (2013) 8:0062 467
R(N19-H20) 0.9924 0.9924 0.9924 1.0065 1.0066 1.0066 R(N19-H21) 0.9924 0.9924 1.0066 1.0067 1.0067 Bond Lengths (R) are given in Armstrong (Å) and atoms labeling according to Fig. 1. Table 1b: Optimized geometrical parameters – Bond angles of Pyrimethamine molecule in different mediums obtained at RHF and B3LYP methods by employing 6- 311++G** basis sets and their corresponding experimental values in gas. B3LYP/6-311++G** 126.5661 126.5661 126.5813 126.5887 126.5882 111.4042 116.4042 116.5302 116.5277 116.5253 117.0147 117.0147 116.8667 116.8614 116.8640 116.0653 116.0653 116.1734 116.1680 116.1686 116.5644 116.5644 116.3674 116.3618 116.3625 116.8374 116.8374 116.7324 116.7293 116.7302 122.4486 122.4486 122.4422 122.4458 122.4461 121.4737 121.4737 121.3714 121.3729 121.3721 115.0879 115.0879 115.5793 115.5766 115.5759 120.7408 120.7408 120.4696 120.4700 120.4766 124.1710 124.171 123.9511 123.9534 123.9475 122.4880 122.488 122.2910 122.2916 122.2910 122.6870 122.6870 122.6697 122.6674 122.6722 121.0529 121.0529 120.9668 120.9751 120.9811 120.9544 120.9544 121.0545 121.0507 121.0451 117.9829 117.9829 117.9685 117.9640 117.9639 121.3749 121.3749 121.3827 121.3856 121.385 121.4024 121.4024 121.4082 121.4102 121.4106 119.1411 119.1411 119.0947 119.0966 119.0967 119.80 119.1812 119.1812 119.1240 119.1256 119.1266 120.9153 120.9153 121.0186 121.0148 121.0139 111.9558 111.9558 112.0507 112.0684 112.0646 119.5466 119.5466 119.4919 119.492 119.4934 119.5380 119.5380 119.4894 119.4924 119.4926 119.4315 119.4315 119.344 119.3386 119.3393 119.1936 119.1936 119.273 119.2755 119.2754 119.4153 119.4153 119.3155 119.3184 119.3161 119.1812 119.1812 119.2758 119.2709 119.2728 120.6316 120.6316 120.7266 120.7265 120.7255 120.1872 120.1872 120.1492 120.1476 120.1476 120.6491 120.6491 120.7408 120.7385 120.7389 120.2098 120.2098 120.1644 120.1648 120.1644 110.5948 110.5948 110.4605 110.4617 110.4679 109.3066 109.3066 109.1122 109.1033 109.1035 The African Review of Physics (2013) 8:0062 468
109.8061 109.8061 109.8103 109.8094 109.8121 107.8799 107.8799 107.7345 107.7305 107.7264 110.1473 110.1473 110.5216 110.5131 110.5133 110.7270 110.7270 110.4946 110.5022 110.5002 111.1655 111.1655 111.1290 111.1442 111.1429 116.7362 116.7362 116.5334 116.4973 116.4914 113.90 120.0663 120.0663 119.5782 119.5473 119.5409 117.1351 117.1351 117.3233 117.3359 117.3108 116.8222 116.8222 116.8992 116.9110 116.8888 118.0941 118.0941 118.3329 118.3405 118.3083 118.1127 118.1127 117.9775 117.9435 117.9371 108.4609 108.4609 108.4215 108.4248 108.4265 109.01 107.9126 107.9126 107.9423 107.9361 107.9357 108.3325 108.3325 108.2345 108.2224 108.2243 Bond Angles (A) are in degrees (˚) and atoms labeling according to Fig.1. 3.2. Optimized geometric properties of
experimental value at the B3LYP/6-311++G** sulfadoxine
level and at the RHF/6-311++G** level, it is 0.114 Å smaller both in the gas phase and dissolved in The geometric parameters of Sulfadoxine molecule water and ethanol. From Table 2a, we also in gas phase, water and ethanol are listed in Table observed that C-N bond lengths on the Pyrimidine 2a. The calculated bond lengths at RHF/6- ring vary slightly. This variation of the C-N bond 311++G** level are slightly smaller (ranging from lengths also suggests that there is an extended pi- 0.01Å to 0.04Å) than their corresponding values electron delocalization over the pyrimidine moiety. obtained at the B3LYP/6-311++G** level. In The bond angles vary from 0.1 to 0.2 degrees in solution (water and ethanol) the bond lengths both RHF and DFT levels of theories with the 6- remain unaffected at the RHF/6-311++G** level of 311++G** basis set (Table 2b). The Phenyl group theory and at the B3LYP/6-311++G** level of and the pyrimidine possibly give added stability to theory. The RHF/6-311++G** and B3LYP/6- the molecule. The Nitrogen atoms (N4, N17, N18 311++G** bond lengths are approximately equal to and N32) and the oxygen atoms (O6, O7, O20 and the experimental values [34,35,36]. The B3LYP/6- O21) play a major role in the electron density 311++G** theoretical calculated values are in configuration. In the water and ethanol dissolved better agreement with experimental values than state, the bond angles remain unaffected both at the their corresponding RHF/6-311++G** theoretical RHF/6-311++G** level and at the B3LYP/6- calculated values. For example in the Pyrimidine 311++G** level of theory as we move from gas ring, the C1-N2 bond length is 0.105 Å, which is phase to water and to ethanol. The bond angles smaller than the C-N experimental value at the (Table 2b) at the RHF/6-311++G** and at the B3LYP/6-311++G** level and at the RHF/6- B3LYP/6-311++G** are approximately equal to 311++G** level. It is 0.124 Å smaller than the C-N the experimental results [34,35,36]. experimental value respectively both in the gas phase and solution in water and ethanol. The C1-N6 bond length is 0.097 Å smaller than the The African Review of Physics (2013) 8:0062 469
Table 2a: Optimized geometrical parameters – Bond lengths of Sulfadoxine molecule in different medium obtained at RHF and B3LYP methods by employing 6- 311++G** basis sets and their corresponding experimental values. Bond Lengths (R) are given in Armstrong (Å) and atoms labeling according to Fig. 2. The African Review of Physics (2013) 8:0062 470
Table 2b: Optimized geometrical parameters – Bond angles of Sulfadoxine molecule in different medium obtained at RHF and B3LYP methods by employing 6- 311++G** basis sets and their corresponding experimental values. 119.9897 119.9897 119.9464 119.9464 119.9764 119.9764 119.6635 119.6635 120.4593 120.4593 119.8619 119.8619 119.8433 119.8433 119.7726 119.7726 119.7614 119.7614 115.6438 115.6438 120.2143 120.2143 120.0275 120.0275 119.8771 119.8771 120.2932 120.2932 120.4659 120.4659 119.1203 119.1203 A(C30-N33-H34) 116.2733 116.2733 116.2733 A(C30-N33-H35) 116.3096 116.3096 116.3096 A(H34-N33-H35) 113.0062 113.0062 113.0062 A(H11-C10-H12) 110.4143 110.4143 110.4143 A(H11-C10-H13) 110.3132 110.3132 110.3132 A(H12-C10-H13) 109.3598 109.3598 109.3598 127.2026 127.2026 A(N2-C3-N18) 118.8657 118.8657 118.8657 A(N2-C1-H7) 116.5600 116.5599 116.5599 A(N6-C1-H7) 116.2354 116.2354 116.2354 116.1156 116.1156 116.5139 116.5139 122.4483 122.4483 118.6516 118.6516 122.0482 122.0482 120.3781 120.3781 120.4724 120.4724 120.3587 120.3587 123.8947 123.8947 117.8637 117.8637 A(N6-C5-O8) 120.0855 120.0855 120.0855 119.2644 119.2644 The African Review of Physics (2013) 8:0062 471
116.3076 116.3076 A(O8-C10-H11) 105.2619 105.2619 105.2619 A(O8-C10-H12) 110.7611 110.7611 110.7611 A(O8-C10-H13) 110.6802 110.6802 110.6802 A(O9-C14-H15) 106.4717 106.4717 106.4717 A(O9-C14-H16) 110.5699 110.5699 110.5699 A(O9-C14-H17) 110.7178 110.7178 110.7178 A(H15-C14-H16) 109.5985 109.5985 109.5985 A(H15-C14-H17) 109.5906 109.5906 109.5906 A(H16-C14-H17) 109.8313 109.8313 109.8313 A(C3-N18-H19) 116.9503 116.9503 116.9503 A(C3-N18-S20) 127.4524 127.4525 127.4525 A(H19-N18-S20) 112.8406 112.8406 112.8406 A(N18-S20-O21) 109.3527 109.3527 109.3527 A(N18-S20-O22) 101.7625 101.7625 101.7625 A(N18-S20-C23) 106.7853 106.7853 106.7853 A(O21-S20-O22) 120.5877 120.5877 120.5877 A(O21-S20-C23) 108.7410 108.7410 108.7410 A(O22-S20-C23) 108.7118 108.7118 108.7118 A(S20-C23-C24) 119.5720 119.5720 119.5720 A(S20-C23-C25) 120.2006 120.2006 120.2006 Bond Angles (A) are in degrees (˚) and atoms labeling according to Fig. 2. 4. Atomic Charges, Polarizability and Hyper-
Hence, it is appropriate to consider the charges calculated by CHELPG scheme of Breneman instead of Mulliken population analysis. Within a Atomic net charges are not quantum mechanical molecular system, atoms can be treated as a (QM) observables, and they cannot be determined quantum mechanical system. On the basis of the directly with QM calculations or by experiments. topology of the electron density, the atomic charges Different methods exist for the estimation of in the molecule can be explained.
atomic charges of the molecular system. Basically, Polarizability is a property that depends on the the atomic charges are best derived by a least second derivative of the energy with respect to the squares fit to the electrostatic potential (ESP), applied electric field. It gives information about the calculated in a large number of points around the molecule of interest [38]. Polarizability plays an important role in the The electrostatic potential derived charges understanding of a large variety of physical using the CHELPG scheme of Breneman [39] at different atomic positions of Pyrimethamine and experimental difficulties obtaining reliable results Sulfadoxine molecules at RHF/6-311++G** and of polarizabilities justify the need of accurate B3LYP/6-311++G** levels of theories have been theoretical results. In some cases, these results are calculated. The Mulliken population analysis partitions the charges among the atoms of a polarizabilities. molecule by dividing orbital overlap evenly components, the average polarizability and the between two atoms. Whereas, the electrostatic potential derived charges assign point charges to fit Pyrimethamine and Sulfadoxine obtained at the computed electrostatic potential at a number of RHF/6-311++G** level and B3LYP/6-311++G** points on or near the Van der Waal surface. This level of theories are listed in Tables 3 and 4, sort of analysis is commonly used to create input respectively. All the six polarizability tensor charges for molecular mechanics calculation. The African Review of Physics (2013) 8:0062 472
components of Pyrimethamine and Sulfadoxine the anisotropy for the molecule at all levels of molecules αxx, αxy, αyy, αxz αyz and αzz components theory. We can also see that the inclusion of changes significantly at the RHF/6-311++G** level B3LYP/6-311++G** polarizability < α> and the anisotropy γ in gas considered here (although they do not follow any phase and in solution phase. We equally observe regular pattern). that the effect of inclusion of electron correlation In the case of Pyrimethamine, the polarizability increases < α > by 17.30 percent for the gas phase, tensor components do not show any change in 17.17 percent when dissolved in water and 17.31 going from gas phase to solution phase at the percent in ethanol whereas γ increases by 45.50 RHF/6-311++G** level but polarizability tensor percent for the gas phase, 45.56 percent when components change slightly at the B3LYP/6- dissolved in water and 45.49 percent when in 311++G** level. From Table 3, we can see that tensor αxx is responsible for the greatest contribution both in the average polarizability and Table 3: Polarizability tensors, average polarizability and anisotropy (x 10-12 esu) of Pyrimethamine using RHF and B3LYP methods by employing 6-311++G** basis set. B3LYP/6-311++G** polarizability < α> and the anisotropy γ in gas polarizability tensor components of Sulfadoxine do phase and in solution phase. We equally observed not show any change in going from gas phase to that the effect of inclusion of electron correlation solution phase at the RHF/6-311++G** level but increases < α> by 4.42 percent for the gas phase, polarizability tensor components change slightly at 0.85 percent when dissolved in water or in ethanol the B3LYP/6-311++G** level. From Table 4, we whereas γ increases by 38.80 percent for the gas can see that the tensor αxx is responsible for the phase, 26.01 percent when dissolved in water or in polarizability and the anisotropy for the molecule at all levels of theory. We can also see that the inclusion of electron correlation affects the average Table 4: Polarizability tensors, average polarizability and anisotropy (x 10-12 esu) of Sulfadoxine using RHF and B3LYP methods by employing 6-311++G** basis set. B3LYP/6-311++G** The African Review of Physics (2013) 8:0062 473
The polarizability and hyperpolarizability of a and when dissolved in ethanol, whereas βzzz molecule are presented as the output in the standard component gives the highest contribution when orientation in triangular and tetrahedral order, dissolved in water. The first molecular hyper- respectively. Hyper-polarizability is very sensitive polarizability is greater at the B3LYP/6-311++G** to molecular structure and highly dependent on the compared to the RHF/6-311++G**, both in gas choice of the basis set [43,44]. Tables 5 and 6 show phase and in solution phase. the diagonal hyper-polarizabilities and the first In the case of Sulfadoxine, the component βzzz molecular hyper-polarizability of Pyrimethamine of the hyper-polarizability gives the highest and Sulfadoxine molecules. Since the values of the contribution to molecular hyper-polarizability at first molecular hyper-polarizability are given in the RHF/6-311++G** level in both gas phase and atomic units, we have thus converted the values in solution phase. At the B3LYP/6-311++G** level, electrostatic units. the component βyyy of the hyper-polarizability gives In the case of Pyrimethamine, the component the highest contribution of the first molecular βxxx of hyper-polarizability gives the highest hyper-polarizability when dissolved in water and contribution to the ethanol and βzzz component gives the highest polarizability at the RHF/6-311++G** level in both contribution in gas phase. The first molecular gas phase and solution phase. At the B3LYP/6- hyper-polarizability is also greater at the B3LYP/6- 311++G** level, the component βxxx of the hyper- 311++G** compare to the RHF/6-311++G** both polarizability gives the highest contribution of the in gas phase and in solution phase. first molecular hyper-polarizability in gas phase Table 5: Components of diagonal hyper-polarizabilities and first molecular hyper-polarizabilities (x 10-33esu) of Pyrimethamine using RHF and B3LYP methods by employing 6-311++G** basis set. B3LYP/6-311++G** -10234.486 698.980 -510.151 11323.963 Table 6: Components of diagonal hyper-polarizabilities and molecular first hyper-polarizability (x 10-33esu) of Sulfadoxine using RHF and B3LYP methods by employing 6-311++G** basis set. B3LYP/6-311++G** -18845.976 -18845.976 -25100.063 2475.790 -11599.634 -11599.634 -15575.985 -18058.020 -18058.020 -28028.844 -28028.844 -37368.636 -2209.536 The African Review of Physics (2013) 8:0062 474
5. Conclusion
F. Kajzar, K. S. Lee and A. K. Jen, Adv.
Poly. Sc. 161, 1 (2003).
We observed that some charge transfer takes place V. Krishnakumar and R. Nagalakshmi, in going from gas phase to solution medium at the Physica B, 403, 1863 (2008).
B3LYP/6-311++G** level of theory. This charge H. Alyar, Rev. Adv. Mater. Sci. 34, 79
transfer is more significant in the case of water than in the case of ethanol. The polarizability of these Y. Zhang and R. H. Holm, J. Amer. Chem. molecules changed slightly following their solution Soc. 125, 3910 (2003).
in different media, in comparison to gas phase, at D. S. Chemla and J. Zyss, Nonlinear Optical the B3LYP/6-311++G** level of theory. Properties of Organic Molecules and The high polarizability values of the molecules Crystals (Academic Press, Orlando, 1987). revealed that the electrostatic and dispersion P. N. Prasad and D. J. Williams, Intro- contribution influence considerably the interaction duction to Nonlinear Optical Effects in of these molecules with other molecules. We also Molecules and Polymers (Wiley, New York concluded that an appropriate treatment of the electron correlation is of fundamental importance J. Zyss, Molecular Nonlinear Optics in order to obtain accurate estimates for the (Academic Press, Boston, USA, 1994). electronic contributions to polarizabilities and N. Venkatram, M. A. Akundi and D. hyper-polarizabilities. Narayana Rao, Optical Express 13, 867
The variation of the C-N bond lengths suggests an extended pi-electron delocalization over the G. W. Ejuh and L. S. Taura, J. Nigerian pyrimidine moiety, which is responsible for the non Association of Mathematical Phys. 20(1),
linearity of these molecules. Due to the large first hyper-polarizability of P. Gunter, Nonlinear Optical Effects and these molecules, we concluded that these molecules Materials (Springer-Verlag, Berlin, 2000). have the potential to produce second order optical D. R. Kanis, M. A. Ratner and T. J. Marks, effects much larger than those obtainable with Chem. Rev. 94, 195 (1994).
inorganic materials which suggests potential for P. Poornesh, G. Umesh, P. K. Hegde, M. G. applications of these molecules in the development Manjunatha, K. B. Manjunatha and A. V. of non linear materials. Hence these molecules, Adhikari, Applied Phys. B. 97, 117 (2009).
which are Malaria drugs also, have application in L. T. Cheng, W. Tam, S. H. Stevenson, G. electro optics devices, photorefractive materials, R. Meredith, G. Rikken and S. R. Marder, J. second harmonics generation, etc. Phys. Chem. 95, 1063 (1991).
Due to the lack of existing experimental or P. S. Liyanage, R. M. De Silva and K. M. N. theoretical results of the hyper-polarizability of De Silva, J. Mol. Struct. (Theochem), 639,
these molecules, we are optimistic that our results will provide a benchmark study for these K. S. Thanthiriwatte and K. M. N. De Silva, molecules, and serve as a reference for other J. Mol. Struct. 617, 169 (2002).
A. D. Tillekaratne and K. M. N. De Silva, J.
Mol. Struct. 638, 169 (2003).
Y. Atalay, D. Avci, and A. Basoglu, Struct. We want to thank the CSIR (Council of Scientific Chem. 19, 239 (2008).
and Industrial Research), New Delhi, for providing C. R. Moylam, R. J. Twieg, V. Y. Lee, S. A. funds with which the Gaussian 03W software was Swanson, K. M. Betteron and R. D. Miller, purchased through Prof. A. N. Singh, Banaras J. Chem. Soc. 115, 12599 (1993).
Hindu University, Varanasi, India. V. P. Rao, Y. M. Cai and A. K. Y. Jen, J. We equally want to thank Prof. A. N. Singh, for Chem. Soc. Chem. Commun. 14, 1689
providing us with the Software and initiating our research in this area. S. Zafar, Z. H. Khan and M. S. Khan,
Canadian J. Pure and Applied Sc. 6(1), 1827
References
H. Alyar, M. Bahat, E. Kasap and Z. Y. Shi, C. Zhang, J. H. Bechtel, L. R. Kantarci, Czech. J. Phys. 56, 349 (2006).
Dalton, B. H. Robinson and W. H. Steier,
Science 288, 119 (2000).
The African Review of Physics (2013) 8:0062 475
H. Soscun, O. Castellano, Y. Berudez, C. K. H. Hellwege and A. M. Hellwege, Landolt-Bornstein, Atom. and Mol. Phys. Alvarado, J. Mol. Struct. 592, 19 (2002).
(Springer-Verlag, Berlin, 1976). H. Li, K. Han, X. Shen, Z. Lu, Z. Huang, W. G. Roussy, J. Mol. Spec. 118, 180 (1986).
Zhang, Z. Zhang and L. Bai, J. Mol. Struct. B. A. Saleh, H. A. Abood, R. Miyamoto and (Theochem), 767, 113 (2006).
M. Bortouzzi, J. Iranian Chem. Soc. 8(3),
B. Champagne and M. Spassova, Chem. Phy. Lett. 471, 111 (2009).
B. Mannfors, K. Palmo and S. Krimm, J. G. W. Ejuh, J. M. Ndjaka and A. N. Singh, Mol. Struct. 556, 1 (2000).
Canadian J. Pure and Applied Sc. 5(2), 1591
C. M. Breneman and K. B. Wiberg, J. Comput. Chem. 11, 361 (1990).
A. Andrea, Adv. Phys. Chem. (Hindawi A. D. Buckingham, Adv. Chem. Phys. 12,
Publishing Cooperation, 2013). M. J. Frisch, G. W. Trucks, H. B. Schlegel, E. F. Archhibong and A. J. Thakkar, J. Phys. G. E. Scuseria, M. A. Robb, J. R. Rev. A 44, 5478 (1991).
Cheeseman, J. A. Montgomery, Jr. T. M. A. Castro and S. J. Canuta, J. Phys. Rev. Vreven, K. N. Kudin, J. C. Burant, J. M. B 26, 4301 (1993).
Millam, S. S. Iyengar, J. Tomasi, V. Barone, D. V. Fernando, A. S. David, T. Yoshinari, B. Mennucci, M. Cossi, G. Scalmani, N. A. Xavier, R. Angel, G. L. Steven and J. R. Rega, G. A. Petersson, H. Nakatsuji, M. John, J. Chem. Phys. 133, 034111 (2010).
Hada, M. Ehara, K. Toyota, R. Fukuda, J. J. Kobus, D. Moncrieff and S. Wilson, J. Hasegawa, M. Ishida, T. Nakajima, Y. Phys. B. Atom. Mol. and Optical Phys. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, 37(3), 571 (2004).
J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Received: 5 October, 2013 Zakrzewski, S. Dapprich, A. D. Danniels, Accepted: 17 January, 2014 M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian Inc., Wallingford CT. (2004). A. D. Becke, Phys. Rev. A. 38, 3098 (1988).
C. Lee, W. Yang and R. G. Parr, Phys. Rev.
B 37, 785 (1988).
S. H. Vosko, L. Wilk and Nusair, Canadian
J. Phys. 58, 1200 (1980).
G. W. Ejuh, J. M. Ndjaka and A. N. Singh,
Global J. Pure & Applied Sc. and Tech.
1(2), 30 (2011).
G. W. Ejuh, J. M. Ndjaka and A. N. Singh,
African Rev. Phys. 6(3), 21 (2011).
G. Herzberg, Electronic Spectra and Electronic Structure Polyatomic Molecules (Van Nostrand, New York, 1966).

Source: http://www.aphysrev.org/index.php/aphysrev/article/viewFile/832/340