craiguniversity.tk

Craiguniversity.tk

This article appeared in a journal published by Elsevier. The attached
copy is furnished to the author for internal non-commercial research
and education use, including for instruction at the authors institution
and sharing with colleagues.
Other uses, including reproduction and distribution, or selling or
licensing copies, or posting to personal, institutional or third party
websites are prohibited.
In most cases authors are permitted to post their version of the
article (e.g. in Word or Tex form) to their personal website or
institutional repository. Authors requiring further information
regarding Elsevier's archiving and manuscript policies are
encouraged to visit:

Author's personal copy
Journal of Chromatography A, 1218 (2011) 556–586 Contents lists available at ScienceDirect Journal of Chromatography A Chromatographic selectivity triangles Andrew R. Johnson, Mark F. Vitha ∗ Department of Chemistry, Drake University, 2507 University Ave, Des Moines, IA 50311, USA 2010 marked the 50th anniversary of the use of selectivity triangles to characterize chromatographic Available online 9 November 2010 phases. Such plots ultimately identify and quantify the blend of intermolecular interactions that occurbetween solutes and solvents/phases. The ﬁrst chromatographic triangle was proposed by Brown and applied to GC stationary phases. Snyder then developed the inﬂuential solvent selectivity triangle (SST) Solvent selectivity triangle based on the gas–liquid partition data of Rohrschneider. The SST was combined with simplex experi- Micellar electrokinetic capillary mental designs to optimize RPLC separations. Subsequent criticisms of the work revolved around the inaccurate predictions that resulted from the SST. These inaccuracies ultimately relate to the inability of the SST to account for the effects of water on the interaction ability of organic solvents. Other crit- System selectivity cubeReversed phase liquid chromatography icisms focused on the selection of the three probe solutes (ethanol, dioxane, and nitromethane) that Gas chromatography were used to deﬁne the apices of the SST. Here, the concerns include the lack of explicit consideration of dispersion interactions and the fact that the three probes do not represent any single intermolecu- Linear solvation energy relationship lar interaction but rather reﬂect a blend of intermolecular interactions. The SST approach was modiﬁed for NPLC by redeﬁning the triangle apices to reﬂect the localization, general adsorption, and basicity ofNPLC mobile phase modiﬁers. Because water is generally absent in NPLC, the triangle approach leads tobetter predictions for NPLC than for RPLC. In subsequent modiﬁcations of selectivity triangles, Fu andKhaledi have created a micellar selectivity triangle (MST) based on linear solvation energy relationships(LSERs) and Zhang and Carr have used the Dolan–Snyder hydrophobic subtraction model to create RPLCcolumn selectivity triangles. We end this review by highlighting more recent methods for comparingselectivities and by discussing a new 3D visualization tool for classifying chromatographic systems ashaving similar or different fundamental energetics of retention and hence having similar or differentselectivities.
2010 Elsevier B.V. All rights reserved.
∗ Corresponding author. Tel.: +1 515 271 2596; fax: +1 515 271 1928.
E-mail address: [email protected] (M.F. Vitha).
0021-9673/$ – see front matter 2010 Elsevier B.V. All rights reserved.
doi:10.1016/j.chroma.2010.09.046 Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Re-evaluation of the SST using solvatochromism and linear solvation energy relationships (LSERs) . . . . . . . . . . . . . . . . . . . . . . . 569 RPLC column selectivity triangle based on the hydrophobic subtraction model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 575 But they didn't ﬁllthe desert with pyramids.
They just built some. Some.
They're not still out there,building them now.
The triangle has been used for tens of thousands of years to represent many rich and complex ideas. Triangles sitting on their base have represented the sun, maleness, and ﬁre while downwards pointing triangles have symbolized the moon, femi- diabolize time. Right? ninity, and water [1]. Alchemists used a horizontal line through We must not curse the passage of time.
an upward triangle to symbolize air, and one through a down- In this, Hecht suggests that while the form of the pyramid had ward triangle to symbolize earth, thus creating triangular symbols great symbolic and structural value, a time eventually came to seek for the four elements: ﬁre, earth, air, and water [2]. There- new activities and new alternatives. Similarly, the chromatographic fore, chromatography could be represented with these symbols triangles that have been built have advanced our understanding because water ﬂowing through layers of earth can cause chemical of selectivity and guided our selections of mobile and stationary phases. In this review, we hope to shine light on those advances.
While the symbolism of triangles has a long history, But we also illustrate the limitations of the technique and propose the application of triangles to chromatography goes back a a new alternative.
mere 50 years. This is quite short in absolute terms, but itrepresents half the life of chromatography [3]. Chromatogra- 2. The importance of the separation factor
phers adopted triangles, prisms, and pyramids for explanatorypurposes principally because they allow three or more col- The separation factor, ˛ (formerly know as the selectivity factor) umn characteristics to be incorporated in two-dimensional is deﬁned as kB/kA where k is the retention factor and A and B refer to two solutes for which B elutes after A. The general resolution We begin this review with a brief description of the importance equation, which relates the plate count (N), the separation factor, of selectivity in chromatography because many triangle schemes retention factors, and resolution (R), shows that resolution is highly aim at understanding the selectivity of one phase relative to oth- dependent on the retention factor, particular at low ˛'s.
ers. The ﬁrst report of triangles in chromatography is then discussed to set the stage for all subsequent developments. We then exam- ine Snyder's key solvent selectivity triangle and how it has been adapted in various ways for the various modes of chromatogra- For example, a change in ˛ from 1.1 to 1.2 nearly doubles the phy (RPLC, NPLC, GC, MEKC). We end by departing from triangles resolution, whereas it is necessary to increase the plate count and propose a different geometric ﬁgure, the cube, for examining four-fold for the same improvement in resolution. Thus, changes and comparing selectivity. This shift can perhaps be best under- to a chromatographic system that differentially affect the reten- stood using an excerpt from Jennifer Michael Hecht's poem "On tion of a critical pair of solutes are the key focus for improving the Strength of All Conviction and the Stamina of Love" (from the separations. For purposes of this review we are taking ‘system' Next Ancient World published by Tupelo Press, copyright 2001.
to include the common variables such as temperature, station- Jennifer Michael Hecht. Used with permission) [4] in which she ary phase, and mobile phase composition that chromatographers frequently change in order to affect selectivity.

Author's personal copy
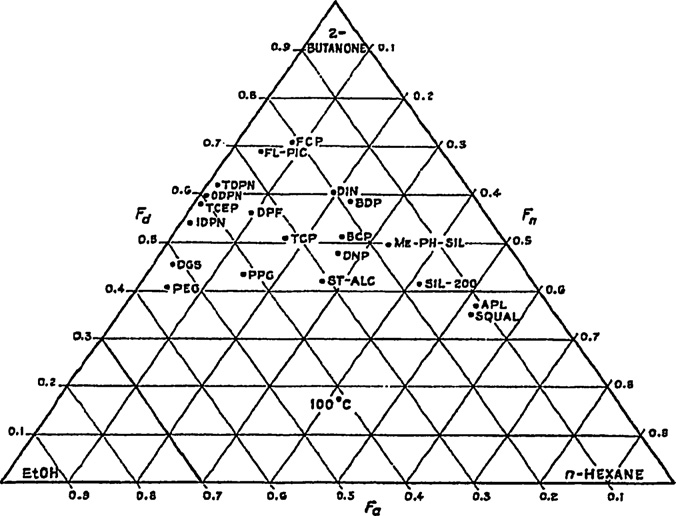
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 1. Classiﬁcation of GC stationary phases by Brown using dioxane, 1,1,2-
Fig. 2. Classiﬁcation of GC stationary phases by Brown using 2-butanone, n-
trichloroethane, and n-decane as test solutes. F hexane, and ethanol as test solutes. F Fa, and Fd are retention n , Fa , and Fd are retention fractions measured fractions measured at 125 ◦C. APL = Apiezon L (Metropolitan, Vickers); XF 1105, XF at 100 ◦C and 67 ◦C from literature sources available at that time. APL = Apiezon 1150 = cyanoethylated silicones (General Electric) with 5% and 50% cyano groups; SQUAL = squalane; Sil-200 = Silicone Me-Ph-Sil = methylphenyl AROCLOR = Aroclor 1262 (Monsanto) chlorinated biphenol; QF1 = ﬂuorinated silicon (Applied Science Labs); m-Bis = m-bis-(m-phenoxyphenoxyl)-benzene (Eastman); BDP = benzyldiphenyl; TCP = tricresyl phosphate (Albright and Wilson); Zonly = Zonyl E7 (Du Pont) DIN = di-n-octyl ester of 4,4-dinitrodiphenic acid; TCP = tricresyl phosphate; pyromellitic perﬂuoro ester; DGS = diethylene glycol succinate (Research Special- PEG = polyethylene PPG = polypropylene ties Co.); PEG = polyethylene glyocol 1500 (Carbide and Carbon); REO = Reoplex 400 IDPN = imino-dipropionitrile; (Geigy); TNB = 1,3,5-trinitrobenzene; FCP = diester of tetrachlorophthalic acid and ODPN = oxydipropionitrile; TDPN = thiodipropionitrile; TCEP = 1,2,3-tris-(2- cyanoethyl)-propane; FL-PIC = ﬂuorine picrate; FCP = diester of tetrachlorophthalic Reprinted from [6], with permission from Elsevier.
acid and 1-H,1-H,5-H-octaﬂuoro-1-pentanol.
Reprinted from [6], with permission from Elsevier.
Comparisons of system selectivity try to help answer the ques- tion: when a given system fails to achieve a desired separation,what does the analyst try next? Because all chromatographic Brown also used different probe solutes. The results of creat- separations are ultimately based on a blend of intermolecular inter- ing the triangle based on n-hexane, ethanol, and 2-butanone are actions (e.g., dipole–dipole, hydrogen bonding, and dispersion), shown in Fig. 2. He noted that "the position of the triangular graph using a system with similar blends of interactions as those demon- for a given phase is determined by the choice of the three test strated by the system that failed is unlikely to provide the desired compounds, and these can be varied to suit a particular problem." results. Instead, systems that are substantially different in their The inﬂuence of the choice of probe solutes is important and will intermolecular interactions must be sought. Thus, the questions be raised elsewhere in this review with regards to characterizing of 1) how to characterize systems in terms of their interaction abil- LC-related systems.
ities and 2) how to differentiate one system from another naturally Interestingly, Brown then used an ‘inverse triangle' (current arise. Selectivity triangle schemes that classify, differentiate, and authors' description) to characterize the intermolecular interaction group chromatographic systems have been used to help answer abilities of individual steroids. This was done by selecting three this question. In this review, we analyze various selectivity triangle chemically different stationary phases – one neutral, one hydro- schemes and how they have been applied to RPLC, NPLC, GC, and gen bond (HB) accepting, and one HB donating – and using them to MEKC systems.
deﬁne the apices of a triangle. The solutes were then characterizedby their afﬁnity fraction, Ai, for each phase via the equation 3. The golden anniversary – 50 years of selectivity triangles
The year 2010 marked the 50th anniversary of the use of triangle schemes to classify chromatographic systems. We make this state-ment based on the fact that the earliest report along these lines that where ‘i' is one of the three columns represented by the numbers we could ﬁnd was from Brown in 1960 [5,6]. He created a triangle 1, 2, and 3. The three phases were SE-30 (silicone), NGS (neopentyl to characterize GC stationary phases by deﬁning a parameter, Fn, as glycol succinate), and QF1 (ﬂuorinated silicone).
Further, by taking the ratio of retention volumes of compounds relative to retention values of an n-alkane of the same size, Brown was able to make the plot shown in Fig. 3. The symbol G is used along where Fn was called the ‘retention fraction', V represented reten- the sides of the triangle because the ratio is ultimately related to tion volumes, and i was n, a, or d which represented the retention the free energy of retention of the functional group.
volumes of non-polar, electron accepting, and electron donating Many of the ideas that Brown introduced would continue to solutes. The solutes chosen to represent n, a, and d were n-decane, appear in one form or another in subsequent papers using triangu- 1,1,2-trichloroethane, and dioxane, respectively. Each phase was lar plots to characterize chromatographic systems. Interestingly, thus characterized by three parameters that varied from 0.00 to though, the exception to this is the application of the triangles in 1.00. The values were plotted at the apices of a triangle, resulting an ‘inverse' manner for the purpose of characterizing individual

Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Table 1
P values for some common solvents [10].
Dimethyl sulfoxide a Estimated values due to missing K values.
that dispersion interactions dominate gas–liquid partitioning, thatthis correction also accounts for dispersive forces that are not com- Fig. 3. Identiﬁcation of homologous series of compounds with various functional
pletely eliminated by the normalization of partition coefﬁcients to groups. G1, G2, and G3 group retention fractions measured at 100 ◦C and 67 ◦C from literature sources available at that time. R = alkyl group; ␸ = phenyl group;PEG = polyethylene glycol.
Each of the solvents in Rohrschneider's collection was char- Reprinted from [6], with permission from Elsevier.
acterized by a parameter, P, deﬁned as the sum of log Kg (P = and stronger hydrogen bond donating/accepting solvents generally 4. Snyder's solvent selectivity triangle
have higher P values as shown in Table 1 [10].
The solvents were further characterized by normalizing log K 4.1. General theory and development for each test solute to P according to Brown's was the earliest report of triangle plots used to char- acterize chromatographic systems, but it was Snyder's solvent selectivity triangle (SST) published many years later that gen- where i = e, d, or n for ethanol, dioxane, and nitromethane, respec- erated more interest and critical examination [7]. Snyder based tively, such that his solvent characterization scheme on Rohrschneider's gas–liquid partition coefﬁcients for three test solutes – ethanol, dioxane, and nitromethane – in 82 common solvents [8]. The three solutes werechosen to probe the ability of each solvent to participate in pro- for all solvents.
ton acceptor, proton donor, and dipolar interactions, respectively.
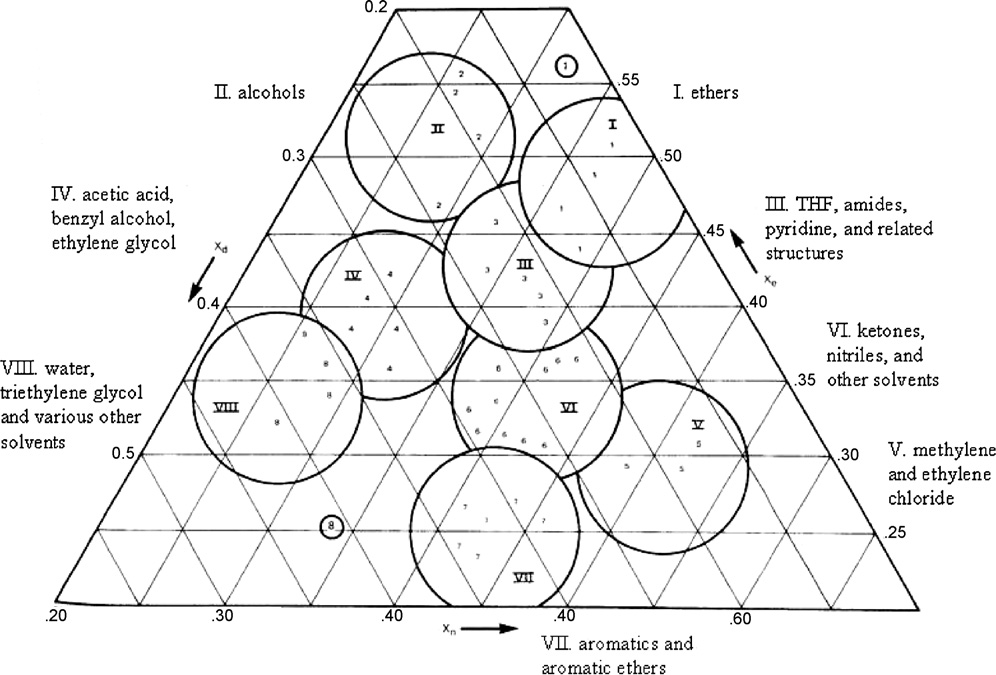
Individual Xi values were used in a triangle plot to group the However, as Cooper and Smith [9] point out, various solvents in Rohrschneider's data set. The resulting plot isshown in Fig. 4 [10]. It is worth noting that this plot is from a ". .in the Snyder system, ‘proton donor characteristics' actually paper published in 1978, 4 years after the original publication, refers to a solvent's ability to interact with a proton acceptor because the actual X (dioxane). It is not an actual measure of proton donating capa- i values used to create the solvent triangle in the original publication were inadvertently incorrect. In Fig. 4, bility, and thus a solvent (or solute) can be classiﬁed as a proton the circles represent groupings of common solvents. For example, donor even though it contains no protons. The same qualiﬁca- group II is comprised of aliphatic alcohols (hence their relatively tion applies to proton acceptors, which are classiﬁed as such based on an ability to interact with a proton donor (ethanol)." e values) and group VII is comprised of aromatic hydrocar- bons, halo-substituted aromatic hydrocarbons, nitro compounds, Put another way, the scales more broadly reﬂect Lewis acidity and aromatic ethers – all highly polarizable compounds. The fact and basicity rather than just interactions formally involving hydro- that similar compounds fall close to one another in the triangle was taken as evidence that the deﬁnition of Xi values does in fact reﬂect To establish his characterizations, Snyder ﬁrst corrected actual chemical properties of the solvents and that the groupings Rohrschneider's distribution coefﬁcients for solvent molecular are useful in identifying similar (or different) solvents in terms of weight. These values were then normalized to the partition coef- their ability to participate in speciﬁc intermolecular interactions.
ﬁcient for a hypothetical alkane of the same volume in order to Snyder's focus in the ﬁrst publication was on solvents that could remove the effects of dispersion interactions, which Snyder con- be used in LC separations. The idea behind the triangle is that sol- tends do not generally contribute signiﬁcantly to selectivity. This is vents in the same groups will provide comparable chromatographic similar to Brown's taking the ratio of retention volumes for solutes selectivity. Therefore, switching from one solvent to another within to those of n-alkanes mentioned above. Snyder gave the resulting the same group would not yield as dramatic a change in selectivity values the symbol Kg. Lastly, a constant derived by considering the as switching to a solvent in a group with very different characteris- Kg values for each solute in saturated alkanes was subtracted from tics (e.g., switching from group I to group VII or VIII). It is critical to each value of log Kg to compensate for incomplete cancellation of note that in this scheme, Snyder modiﬁed the traditional deﬁnition dipole induced–dipole interactions, entropy, and other effects. A of chromatographic selectivity with its focus on the separation of different constant is used for each of the three test solutes. The two different solutes in a particular solvent system, to one based derivation of the constants is described in the original publications on comparing two (or more) different solvents – or more broadly, [7,10,11]. In essence, it makes the Kg values for each test solute very two different chromatographic systems – and how they might sep- close to zero in alkane solvents. It is reasonable to suggest, given arate a set of solutes through different blends of intermolecular

Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 4. Snyder's solvent selectivity triangle. Reproduced from the Journal of Chromatographic Science by permission of Preston Publications, a division of Preston Industries,
Inc. The solvent listings along the axes were added by the present authors.
interactions. For example, he differentiates between the strength Initromethane = 1.18Initropropane, allowing for Initropropane to be of a solvent and its selectivity by stating "The strength of a solvent calculated if it were not in the data sets of Rohrschneider [8] or depends on its "polarity", or ability to preferentially dissolve more McReynolds [12,13] for various phases. Based on these log Kg val- polar compounds such as nitriles and alcohols. Solvent selectivity ues, the parameters for Xi could be calculated for GC phases. Snyder refers to the ability of a given solvent to selectively dissolve one presented Xi values for diethylhexyl sebacate, diisodecyl phthalate, compound as opposed to another, where the ‘polarities' of the two tricresyl phosphates, carbowax 20, diethyleneglycol succinate, and compounds are not obviously different" [7].
While the 1974 publication explained the derivation of the Klee et al. [14] developed a selectivity triangle for GC phases parameters and subsequent triangle plot, the 1978 publication is (1) Most importantly, whereas the 1974 publication focused on common, volatile organic solvents related to LC, the 1978 pub- In an interesting modiﬁcation of the SST for GC phases, they lication was extended to include GC stationary phases, used the sum of the three Ii values to add another dimension to (2) Snyder offers a defense of using just three test solutes to clas- the triangle plot as shown in Fig. 5. This was done to indicate the sify solvents. Two additional solutes (methylethyl ketone and overall polarity of phases in addition to the relative importance of toluene) were examined as part of this analysis, the various speciﬁc interactions. Klee et al. also noted that for the (3) Assertions are made regarding the relative unimportance of best range of GC selectivities, it would be ideal to have phases with dispersion interactions to selectivity, and I values in combination with points near the apices of the (4) Snyder defends the groupings by showing the overall deviations triangles, with the implication being that at that time, such a range of Xi values from their averages are generally within 0.03 units of phases was not available.
(one SD), or 0.015 if groups are further subdivided.
Thus, the 1978 publication simultaneously corrected, reﬁned, bolstered, and expanded the SST scheme presented in the 1974publication.
4.2. The SST and GC phases As noted above, Snyder extended the SST to GC phases [10] by using the conversion where ‘i' is ethanol, dioxane, or nitropropane, I i = In,PH − In,SQ where PH stands for the phase of interest and SQ repre- Fig. 5. A selectivity prism in which the sum of retention indices (
nitromethane, and dioxane is used to add another dimension to a selectivity triangle sents squalane, and ‘b' is the logarithm of the retention time deﬁned using those same solutes (see text for deﬁnitions of Xe, Xd, and Xn). CW- increment per methylene unit added to a solute and is spe- 20M = Carbowax 20M.
ciﬁc to the phase being studied. It was further noted that Reprinted from [14], with permission from Elsevier.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 4.3. Teas diagrams While the rest of this review focuses on the development, appli- cation, and analysis of chromatographic selectivity triangles, webrieﬂy note here that Teas [15] published a solvent triangle in theyears between the appearance of Brown's and Snyder's work. Histriangle was based on the work of Hansen [16] who used solubil-ity parameter and regular solution theory to deﬁne three solventparameters, ıd, ıp, and ıh to quantify the dispersion, polarity, andhydrogen bonding properties of solvents, respectively. Teas usedthese three parameters as the axes for his solvent triangle. Heapplied his triangle to make predictions about which solvents orsolvent mixtures would solubilize polymeric resins. It is interest-ing to note that Teas diagrams (as they are called) are used in theﬁeld of art restoration to guide the selection of solvents to removevarnishes from old paintings [17]. For example, a Teas diagram wasused in the 1994 restoration of Johannes Vermeer's The Girl with aPearl Earring [18].
Fig. 6. Simplex experimental design involving seven training mobile phases (1–7)
and three mobile phases used to test the accuracy of the predictions. A, B, and C were
5. Impact of Snyder's solvent characterization scheme
mixtures of A = methanol/water (63:37%, v/v), B = tetrahydrofuran/water (39:61%,v/v), and C = acetonitrile/water (52:48%, v/v).
Reprinted from [19], with permission from Elsevier.
5.1. The chromatographic optimization factor A number of publications using Snyder's solvent triangle as a tion schemes involving three mobile phases, the three conﬁrmatory basis for optimizing chromatographic separations were published analyses were dropped, leaving a seven-run optimization design. In in the 1980s. The main impact of Snyder's work was in deﬁning the COF in this study, B = 0 and A = 1.0, indicating that time of anal- three solvents that were deemed to have different selectivities. For ysis was not a concern and the separation of all adjacent pairs was example, in RPLC, methanol, acetonitrile, and tetrahydrofuran were taken to be equally important. The COF was evaluated at three Rid located in fairly distinct regions of the solvent triangle. For this and values of 1.2, 1.8, and 2.4 and plotted in a triangle scheme shown in other reasons, these solvents were used in addition to water to Fig. 7. The optimum separation was found with 61%ACN : 39%THF.
optimize separations, often to the exclusion of other solvents.
Consistent with this, Glajch et al. proposed the chromatographic 5.2. Overlapping resolution mapping for RPLC optimization factor (COF) as the basis for triangles related to max-imizing separations [19]. The COF is deﬁned as Due to limitations of the COF and difﬁculty extending it to mixtures with more solutes, the authors developed overlapping resolution maps (ORM) [19]. The ORM compares the resolution of every pair of peaks in a chromatogram obtained for each sol- vent mixture tested. A contour triangle map is used to estimate the resolution for each pair in all compositions. Any area of the i is the resolution of the ith pair of solutes in a mixture, Rid is the ideal desired resolution, t map with a resolution less than the desired resolution for that pair M is the maximum acceptable analysis is shaded in and areas with "excess" resolution are left clear. The L is the experimental time. Ai is an arbitrary weighting factor that allows greater emphasis on some critical pairs relative maps for all adjacent pairs of compounds are overlaid and any area to others. B is also an arbitrary weighting factor. The function is that remains unshaded provides a solvent composition that could constrained so that if R separate the mixture with the desired resolution. Such an analysis i > Rid then Ri is set equal to Rid, and if tM > tL, tM is set equal to tL. Using these deﬁnitions and constraints, theCOF goes to zero for separations that meet all of the requirements.
Negative values indicate less desirable separations – the larger thenegative, the less desirable. This approach grew out of the chro-matographic response functions (CRF) of Morgan and Deming [20]and subsequent improvements proposed by Watson and Carr [21].
Glajch et al. acknowledge limitations of the COF as the basis forsolvent optimization. For example, it does not explicitly take notewhen peak elution order changes with different mobile phases. Fur-thermore, separations with overlapping peaks can have the sameCOF value as those with the expected number of peaks because themodel does not ‘know' how many peaks should be found – it simplymeasures the separation of the observed peaks.
Also in this report, a simplex design [22] involving ten test runs, shown in Fig. 6, was used to optimize a three-solvent sys-tem (represented by A, B, and C) for a solute mixture of ninesubstituted napthalenes. In this ﬁgure, A, B, and C were mixturesof methanol/water (MEOH, 63:37%, v/v), tetrahydrofuran/water Fig. 7. Chromatographic optimization factor (COF) plot based on simplex exper-
(THF, 39:61%, v/v), and acetonitrile/water (ACN, 52:48%, v/v), imental design for the separation of nine substituted napthalenes. MEOH :methanol/water 63:37% (v/v); THF : tetrahydrofuran/water, 39:61% (v/v); and respectively. Seven of the runs (labeled 1–7) were used to make pre- ACN : acetonitrile/water, 52:48% (v/v). Conditions: 15 cm × 4.6 cm Zorbax-C8 col- dictions of separations while the remaining three runs (8–10) were umn, 2.0 mL/min, 40 ◦C, UV photometer, 254 nm.
used to test the accuracy of the predictions. In subsequent optimiza- Reprinted from [19], with permission from Elsevier.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 8. Overlapping resolution maps (ORM) based on simplex experimental design
for the separation of nine substituted napthalenes. Shaded areas represent sol-
vent mixtures that will not resolve the indicated pair to a resolution of 1.5.
The ﬁve most difﬁcult solute pairs to resolve are shown in the plot. MEOH :
methanol/water 63:37%, (v/v); THF : tetrahydrofuran/water, 39:61% (v/v); and
ACN : acetonitrile/water, 52:48% (v/v). Conditions: 15 cm × 4.6 cm Zorbax-C8 col-
Fig. 9. A three-dimensional rendering of the ORM created by displaying the resolu-
umn, 2.0 mL/min, 40 ◦C, UV photometer, 254 nm.
tion for the most poorly resolved solute pair in the vertical direction. Based on the Reprinted from [19], with permission from Elsevier.
data from the previous ﬁgure.
Reprinted with permission from [24]. Copyright 1983 American Chemical Society.
was performed with the retention data for the nine naphthalenederivatives to yield the triangle plot in Fig. 8 [19]. On this plot, the competition for surface sites with solutes which can also localize.
optimum solvent mixture that was predicted by the COF method The differences in the speciﬁc type of localization yield different (designated with a ⊗) is included in the solvent mixture region effects on selectivity. A third class of solvents which do not demon- generated by ORM. The authors go on to demonstrate their method strate localization effects, but rather appear to adsorb to the surface using a literature data set of ﬁfteen benzene derivatives [23].
in a more general manner was also identiﬁed. The three solvent For this approach to work, it is necessary to perform peak match- properties (i.e., non-localizing, localizing basic, and localizing non- ing for each of the seven starting runs in order to identify any peak basic) were used as the apices to create an NPLC-speciﬁc triangle.
cross-overs. Then the retention times and peak widths (or calcu- Methylene chloride, MTBE, and ACN were used to represent the lated peak widths) can be used to calculate the resolution of any three properties, respectively, in a simplex optimization scheme.
critical solute pairs for every composition within the triangle.
We go into more detail about the inﬂuence of localization effects on This approach was based on the optimization of only three selectivity below. What is important to note here is the application solvents (mixed with the fourth solvent, water). The choice of of optimization schemes based on selectivity triangles to normal optimizing three parameters was based on the conclusion from phase separations.
the original SST work that only three general solvent charac-teristics affect selectivity. Better resolution may be achieved by 5.4. Gradient elution overlapping resolution mapping including more solvents or optimizing any additional variablessuch as temperature that also inﬂuence selectivity. However, Kirkland and Glajch extended the ORM approach to include gra- including additional variables inﬂates the number of ‘training chro- dient elution [26]. They did so by adding a third dimension – solvent matograms' required by the simplex design, with a subsequent strength – to the two-dimensional triangle plots. In the 2D plots, all increase in the labor and time required to optimize the separation.
three apices were selected to have comparable solvent strengths.
In 1983, Glajch and Kirkland noted that the effects of different Therefore, all that varied within the triangle space was selectivity.
stationary phases, temperature, pH, ionic effects, and secondary By turning the triangle into a prism (see Fig. 10), solvent strength equilibria such as ion-pairing could be incorporated into LC opti- was added along the third dimension such that any vertical slice mization schemes [24]. This publication includes a 3D visualization of the prism parallel to the ends of the prism reﬂects mobile phase involving triangle schemes (see Fig. 9). It resulted from adding the systems of comparable solvent strength. Varying solvent strength actual predicted resolutions in the third dimension rather than just and selectivity allows gradient elution separations to be optimized shading in regions below a certain threshold value as in the 2D in much the same manner as described for isocratic optimizations.
triangle plots shown in the previous ﬁgure.
Seven mobile phase gradients were used to collect resolution datafor fourteen compounds. Estimates of resolution at other gradients 5.3. Overlapping resolution mapping for NPLC were obtained via quadratic equations based on the original sevencompositions and used to create resolution contour maps for indi- Glajch et al. extended the ORM approach to optimizing the vidual pairs of solutes. An overlapping resolution map (now 3D) NPLC separation of thirteen substituted naphthalenes on bare sil- then indicates the position along the gradient and the solvent com- ica particles [25]. The selection of the three mobile phase additives position that yields the maximum predicted resolution. While each (methylene chloride, acetonitrile, and methyl tert-butyl ether, all slice of the prism represents a different solvent strength, proceed- mixed in hexane) was based on a new triangle scheme designed to ing through the prism along any one line of solvent strength (e.g., account for effects that are important in NPLC. Speciﬁcally, basic line 7 in Fig. 11) does not change the selectivity of the mobile phase polar solvents (e.g., methyl tert-butyl ether, MTBE) localize on [26]. Thus, analyses using such gradients were termed ‘isoselec- the solid surface through direct hydrogen bonding with the sur- tive multisolvent gradient elution' (IMGE). The authors note that face. Other solvents with diminished basicities, such as acetonitrile the chromatogram obtained with the predicted gradient achieved (ACN), also localize on the surface but in a different manner than a resolution of 2.0 or greater for the fourteen compounds in under do the basic polar solvents. Both types of solvent localization create ﬁfteen minutes (15 cm × 0.46 cm column, Zorbax C-8, 3.0 mL/min, Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 10. Solvent strength prism for gradient elution with an isocratic selectivity
triangle for one solvent strength. Apices are methanol (MeOH), acetonitrile (ACN),
and tetrahydrofuran (THF).
Reprinted from [26], with permission from Elsevier.
35 ◦C, particle size not shown) and that this was better than any ofthe seven gradients used to establish the analysis.
It is more typical in gradient elution to simultaneously vary selectivity and solvent strength. Kirkland and Glajch used the term‘selective multisolvent gradient elution' (SMGE) to describe thisapproach [26]. Visual inspection of the seven initial chromatogramsresulted in a gradient depicted in Fig. 12. The chromatogramobtained with this gradient yielded even better separation for allpeaks and resulted in a different elution order for some of thepairs. The authors did note, however, abrupt baseline changes cor-responding to the abrupt changes in mobile phase compositiondepicted in the ﬁgure. Nonetheless, with seven training gradientsselected based upon Snyder's original selectivity triangle (to selectthe three organic solvents) and simplex experimental design pro- Fig. 12. Representation of solvent program for step-selectivity gradient solvent
system. (—) Water; (· · ·) methanol; (- - -) acetonitrile; (-·-) tetrahydrofuran.
tocols, the authors were able to systematically select a quaternary Reprinted from [26], with permission from Elsevier.
mobile phase gradient that allowed for complete separation of allcompounds.
presented an approach that slightly reduced the complexity of 5.5. Additional work on optimizations calculation and the number of training chromatograms required(down to four) to obtain optimal solvent strength and selectivity for Shortly after Kirkland and Glajch published the prism scheme isocratic separations. They demonstrated this approach with a rela- for optimizing gradients elution, Sticher and co-workers [27] tively simple mixture of four ﬂavonoid glycosides. Different groupshave suggested from four to ten or more training experiments.
The choice naturally depends on the accuracy of the predictionsthat is required. More training experiments will be required forgreater accuracy, separations with larger numbers of analytes, andseparations involving analytes with closely related structures.
Whereas Glajch, Kirkland, Squire, and Minor's ORM approach strives to obtain a solvent mixture that maximizes COF (related toln[Ri/Rid]) for all components (if weighting factors are not used),O'Hare and co-workers modiﬁed this approach to focus on relativeretention rather than on absolute retention as a function of solventcomposition [28,29]. In their reports, the parameter that is relatedto solvent composition is ln(RTo/RTn) where RTo is the retentiontime of an internal standard and RTn is the retention time of various Fig. 11. Experimental design for seven gradient elution chromatograms to obtain
components. Separate polynomial equations are obtained for each data for optimization calculations. See original reference for solvent compositions.
compound in the mixture based on seven training chromatograms Reprinted from [26], with permission from Elsevier.
selected in a manner akin to that used by Glajch et al. based on Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 SST to RPLC arise largely because of the effects of water, althoughchallenges were also made to the application of triangles to NPLCand GC. In RPLC, water is present in varying amounts in the mobilephase. This has three main effects: (1) increasing water contentincreases the overall polarity of the mobile phase and thereby altersthe selectivity of the separation, (2) the water modiﬁes the abilityof the organic mobile phase additives to interact with solutes andthese alterations affect different solutes to different extents and (3)the water itself interacts differently (i.e., selectively) with differentsolutes. None of these effects is captured in the SST because the SSTwas based on pure organic solvents, not solvents modiﬁed withwater.
The work of Carr and co-workers [30,31] and El Seoud and co- workers [32] illustrates some of these complexities. Non-linearitiesin the frequency of maximum absorbance of solvatochromic dyesvs. percent water in methanol/water and acetonitrile/water mix-tures are observed. These non-linearities are attributed to bothmicroheterogeneity and to preferential solvation effects [30–32].
Furthermore, the nature and extent of these effects depend bothon the organic modiﬁer and the composition of the mixture. Forexample, acetonitrile/water mixtures were found to be dominatedby solvent clustering between 30% and 80% acetonitrile [32–37].
In methanol/water mixtures, however, Shulgin and Ruckenstein[38] assert that if any clusters exist, they are small. While solventclustering may not be extensive in methanol/water mixtures, the Fig. 13. Statistical design for optimizing isocratic elution using four solvents. The
spectroscopic studies of Carr and co-workers [30,31] and El Seoud numbers indicate individual mobile phases in which retention data for all solutes and co-workers [32] suggest that preferential solvation of solutes must be obtained. The authors note that in RPLC, some water-rich and water- may still occur. Regardless of which effects exist within speciﬁc poor phases can be eliminated, reducing the number of training chromatogramsto twelve.
aqueous mixtures, neither the effects of microheterogeneity nor Reprinted from [28], with permission from Elsevier.
preferential solvation on solute retention are incorporated in theSST. Thus, the SST may not produce accurate predictions of selec- simplex designs. The authors stated interest was in analyzing mix- tivities when aqueous mobile phases are used. Examples of this are tures of adrenocorticol steroids, with a primary requirement "to discussed below.
separate and measure aldosterone without interference from other The failures of the SST arising from the presence of water in unrelated steroids [that were in the mixture] together with the RPLC do not carry over to NPLC because the water content in NPLC resolution of 18-hydroxysteroid congeners of aldosterone, 18OH-B mobile phases is generally minimized. Thus, predictions of NPLC and 18OH-A." This goal necessitated the shift from overall reso- mobile phase selectivity based on triangle schemes, when speciﬁc lution to one that required speciﬁc attention on critical solutes, solvent localization and basicity effects are taken into account, are hence the emphasis on individual retention times rather than on generally much more reliable than those in RPLC.
resolution mapping for all components obtained via an ORM. The The other major challenges considered in this section revolve authors acknowledge that ORM can be adjusted to focus on crit- around (1) the inﬂuence of interfacial adsorption and inadequate ical analytes by excluding solvent selectivity areas corresponding retention of the test solutes in GC and (2) the number and spe- to pairs of minor importance, but they noted some problems asso- ciﬁc nature of the test solutes used to create selectivity triangles.
ciated with this for their particular sample of interest. Using their The focus here is on the importance of incorporating dispersion approach, they were able to identify a mobile phase composition interactions and the inﬂuence that using different test solutes has that achieved their goals.
on the position of solvents within the triangle (i.e., their overall Interestingly, they extend their analysis to consider the require- classiﬁcation and grouping).
ments of optimizing four-component systems (the above studieshave four-components – water, methanol, THF, and ACN – but each 6.1. Steroids and polystyrene oligomers apex of the triangle upon which the approach is based is actuallya mixture such as water/MeOH, etc.). A four component system While Snyder's solvent selectivity triangle had an important could include the four pure solvents, or perhaps involve another impact on LC solvent selection as demonstrated by the above opti- water/solvent mixture such as water/dioxane. If a four-component mization methods, others discussed the limitations and failures of system were considered, simplex optimization dictates the need the approach. For example, West described the failure of the solvent for ﬁfteen training chromatograms as shown in Fig. 13 [28]. The selectivity triangle to group solvents according to their selectivity time requirements and subsequent complexity of the data analy- for resolving aromatic compounds and steroids using RPLC [39,40].
sis for such an optimization become much more cumbersome than Lewis et al. made the same observation for polystyrene oligomers those for ternary systems and often are unnecessary, particularly because most of the theoretical optimizations we have focused on In his work related to steroid separations in RPLC, West noted here result in isocratic mobile phases and therefore do not take that the slopes of steroid retention factor (measured using 2- advantage of the practical beneﬁts of gradient elution.
ketoalkanes as standards akin to Kovats GC-based retention indicesusing n-alkanes) vs. volume fraction of organic solvent showed con- 6. Failures of and modiﬁcations to the selectivity triangle
siderable variability for solvents from the same selectivity group.
Speciﬁcally, he noted the average slope for twelve steroids was 2.3 In this section we discuss challenges to the SST that appeared times greater for 1-propanol than for methanol, which are in the in the literature. The problems that were found when applying the same solvent group in the triangle. He also noted that the slopes Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 were sometimes more similar for solvents in different groups than contribute to experimentally observed selectivity for more com- within groups. For example, the average slope (again over twelve plex molecules." [40] steroids) for 2-methoxyethylacetate (Group VI) was closer to that In fairness to Snyder's selectivity triangle, it must be pointed out for tetrahydrofuran (Group III) than it was for acetonitrile (also that it was not intended to be used in the way West applied it. It Group VI). Other such examples are provided in his article [40].
was a general scheme for classifying solvents to facilitate the selec- The resolution of particular pairs of steroids in aqueous mobile tion of solvents that are broadly different in the way they interact phases with different organic modiﬁers of comparable solvent with a wide range of solutes of varying chemical characteristics. It strength was also studied. For spironolactone and ethisterone, the was not designed to predict the best solvent for resolving individ- resolution obtained with 2-ethyoxyethanol, 2-methoxyethanol, ual pairs of closely related solutes. Nevertheless, West's ﬁndings and tetrahydrofuran (all in Group III) was 0.68, 1.15, and 3.26, call into question the overall similarity of some of the solvents in respectively. It should be noted that the mobile phase com- various groups, as well as highlight the potential effects of water position was adjusted such that the ﬁrst peak eluted with a and dispersion interactions on selectivity (see below for more on retention factor of 2.00 ± 0.03 to ensure comparable mobile phase the topic of dispersion).
strengths. Within Group VI solvents, the resolution with diox- The work of Martire and co-workers [37] is interesting as it ane, 2-methoxyethylacetate, and acetonitrile was 1.70, 0.87, and relates to West's criticism that the SST fails to account for the role 0.59, respectively. West also notes that the resolution obtained of the stationary phase. Using alkylbenzenes as test solutes, activ- with solvents from different groups is often more similar than ity coefﬁcients from the literature, and experimental measures of that obtained with solvents within the same group. For example, retention volumes, Martire et al. calculated contributions to the the resolution of prednisone and hydrocortisone in THF (Rs = 1.81) methylene unit selectivity arising from the mobile and station- and 2-methoxyethanol (Rs = 1.93), both from Group III, was more ary phases as a function of percent modiﬁer in methanol/water similar in ethanol (Rs = 1.88) from Group II than in another group and acetonitrile/water mobile phases. They show that the sta- III solvent, 2-ethoxyethanol (Rs = 2.54). Similar observations were tionary phase contribution with both modiﬁers is comparable in made for spironolactone and ethisterone.
magnitude and essentially constant from 5% to 60% water. The con- West states that these observations "contradict the theory of the tribution from the mobile phase, however, varies signiﬁcantly over solvent selectivity triangle concept" [40] and then goes on to sug- that range, and is considerably larger than the stationary phase gest that the discrepancies result from the fundamental assumption contribution at all compositions. Tan and Carr provide a compa- that dispersion interactions do not play an important role in deter- rable result based on the analysis of mobile and stationary phase mining solvent selectivity for solutions of polar solvents. Certainly, cohesive energy densities for systems involving methanol, ace- given the structural similarity of the steroids in this study, it is tonitrile, and tetrahydrofuran. They state that "As the fraction of reasonable to suggest that their overall characteristics regarding water is increased, the cohesive energy density of the mobile phase polarity and hydrogen bonding are comparable enough that even increases substantially. However, changes in the cohesivity of the small differences in dispersion interactions in the solvents, if not bonded phase, which are largely controlled by the sorbed solvent, accurately corrected for, could play a critical role in solvent selec- are minor" [42]. These results suggest that assuming a constant (and relatively unimportant) contribution to solvent selectivity arising Focusing on dispersion only, however, neglects the more impor- from different modiﬁcations of the stationary phase due to differ- tant effects that water has on solvent selectivity. Speciﬁcally, ent organic additives may be a reasonable approximation. Here Snyder's groupings are based on Rohrschneider's data, which were again, it is important to remember that the SST ultimately deals collected for pure solvents. In contrast, West used binary mix- with solvent selectivity. Thus, while the stationary phase clearly tures of solvents with water as the diluent. It is well known that makes an important contribution to the overall retention of solutes, water is hardly an ‘inert' solvent and can signiﬁcantly alter the stationary phases modiﬁed with different solvents may be compa- properties of bulk organic solvents. Furthermore, it does so in dif- rable enough in their characteristics that differences in the mobile ferent ways depending on the organic solvent and the percent phases alone are more important to overall selectivity differences.
composition of the mixture as discussed above with regards to pref- If this is the case, West's concerns about the role of the stationary erential solvation and microheterogeneity. These variations could phase may be overstated. We note here, however, that the changing very well cause a difference between the group that a pure sol- structure of the stationary phase and the modiﬁcation of the alkyl vent would be in compared to that of aqueous mixture of the chains and surface silanol groups by sorbed solvents is clearly an same solvent. The adjustment of solvent strength to obtain a reten- important aspect of RPLC retention. Tan and Carr [42] provide an tion factor of 2.00 for the earliest eluting peak is an arbitrary extensive discussion of the inﬂuence of sorbed water and modiﬁer choice and required different amounts of water for different sol- on mobile and stationary phase properties and how they contribute vents. Clearly, the amount of water and its alterations of organic to changes in solute retention. An analysis of the effects of solvent solvent characteristics will signiﬁcantly impact retention of polar sorption in general, and of their work in particular, is outside the and hydrogen bonding solutes as compared to its impact on non- scope of this review, but the reader is encouraged to consult their polar compounds. Thus, varying amounts of water will inﬂuence the selectivity of the separation in ways that the SST scheme In fairness to West, it must be noted that he acknowledged for pure solvents does not incorporate and cannot accurately the possibility that the structural similarity of the steroids and polystyrene oligomers used in previous studies was the major fac- West does not comment directly on the inﬂuence that different tor behind the discrepancies between groupings and selectivities amounts of water in the mobile phase have on selectivity. But in that he observed. To address this, he conducted another study with recognition of the possibility that dispersion plays an important sixteen aromatic compounds (13 monosubstituted and three posi- role in selectivity, and also in consideration of the assumption that tional isomers) using aqueous mobile phases of twelve solvents the stationary phase does not affect separations, he states ranging in P values from 3.9 to 7.2 from three groups in the solvent "Perhaps these assumptions have resulted in an oversimpliﬁed triangle (II, III, and VI). The binary mobile phases were adjusted to approach to characterizing selectivity, or perhaps the three test yield retention factors of 4.00 ± 0.04 for benzene in an effort to keep solutes that were used to establish the solvent triangle do not solvent strength constant. Again West used retention indices based adequately encompass all of the important characteristics that on 2-ketoalkanes to measure retention. He noted that the retention Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 indices of some compounds in some solvents were more compa- the molar volume and the dispersion-related solubility parameter rable in solvents from different groups than in solvents within the for the solutes, and (4) differences in the solvents' solubility param- same group, leading him to state "in general, there was very lit- eters. In others words, according to this theory, dispersion effects tle or no correlation between retention indices and the solvents do not cancel as they relate to solvent selectivity. The extent of grouped according to the selectivity triangle concept" [39]. He also their importance depends on the combination of solutes and sol- measured resolution of various compound pairs, noting vents being considered. We did some simple calculations involvingvarious combinations of hexane, pentane, benzene, and toluene as "the results of this study conﬁrmed that solvents in the solutes and solvents. The most dramatic effect was observed using same selectivity group seldom give similar resolution, even at hexane and toluene as solutes and pentane and benzene as solvents.
consistent solvent strength. .Numerous examples of extreme In this case, our calculations using regular solution theory sug- variation of R with the solvent groups are evident, with res- gest that the selectivity for these solutes in pentane will be nearly olution frequently being more alike for solvents classiﬁed in four times greater than in benzene. Using benzene and toluene as different groups than for those within a given group." solutes and hexane and pentane as solvents led to the result that Here again, different amounts of water were required to achieve the selectivity in pentane will be only 1.0026 times greater than the comparable solvent strengths for the elution of benzene. As noted selectivity in hexane. So even from these systems, in which disper- above, water preferentially alters the selectivity of polar and hydro- sion is the only dominant intermolecular interaction, it is difﬁcult gen bonding solutes. It does so through the three mechanisms to state how important dispersion interactions are to determining discussed in the introduction to this section, namely, a general solvent selectivity. It can be said that they do not cancel, but the increase in mobile phase polarity with increasing water, modiﬁ- magnitude of their effect varies with speciﬁc systems.
cation of the solvent interaction abilities, and direct interaction Two things must be noted. First, we have considered systems with solutes. This suggests that an expansion of Snyder's triangle in which dispersion is the main intermolecular interaction. It may to include mixed solvents would provide valuable chemical insight be that the contributions of dispersion to solvent selectivity are into the effects of water on the properties of common organic sol- quite small compared to the contributions from dipole–dipole and vents. It would also increase the predictive power of the triangle hydrogen bond interactions when polar and hydrogen bonding with practical implications for RPLC.
solutes and solvents are considered. Second, the above results West, however, might reject this idea as his writings indicate a were based solely on regular solution theory with no further nor- fundamental objection to the construction of the triangle, namely malization or attempts to cancel dispersion interactions. Snyder, that "it is constructed using data that does not correlate with however, in the development of the triangle, corrected Rohrschnei- resolution" and that speciﬁcally "the use of fractions of summed der's partition data for differences in solvent molecular weight retentions actually serves to hide differences in selectivity by mask- and then normalized the results to the partition coefﬁcient for a ing absolute differences in retention units" [39]. He notes that these hypothetical alkane of the same volume. Following this, a con- criticisms extend to the classiﬁcation of NPLC solvents and GC sta- stant derived by considering the partitioning of solutes in saturated tionary phases as well. West proposes instead that his approach alkanes was used to compensate for incomplete cancellation of (not discussed here but developed in his publication) using dif- dipole induced–dipole interactions, entropy, and other effects. In ferences in retention indices, which clearly shows the selectivity these ways, the data treatment involved many steps that are differences between solvents, correlates better with experimen- not present in regular solution theory. Thus, while according tally observed resolution and this provides better predictions and to theory, dispersion interactions should play a role in solvent better separations.
selectivity, Snyder took many steps to reduce or eliminate their In contradiction to West's claims, Snyder et al. [43] cite a presen- tation given by Starcevic at the 15th International Symposium on It is also worth examining the work of Meyer and co-workers in Column Liquid Chromatography (Ref. [23] in the cited work) that this discussion of dispersion interactions. They quantiﬁed the rel- the selectivities for a different series of compounds did correlate ative importance of various intermolecular interactions in a series with predictions from the SST. Snyder et al., however, do not spec- of papers that examined the cohesive energies (Ec) of polar organic ify the series, and the authors of the present article did not ﬁnd any liquids [46–49]. By examining the densities of polar organic com- publications by Starcevic to support the claims.
pounds (e.g., 2-ketones) compared to parafﬁns, the authors wereable to estimate the contributions of orientation (dipole–dipole), 6.2. A note about dispersion induction (dipole-induced dipole), and dispersion energies to thecohesion of the bulk solvents, deﬁned as "the energy required to We mentioned above that the SST is based on the assertion that separate the component molecules to inﬁnity without changing dispersion interactions in solutions of polar solvents do not con- the average internal energy of the individual molecules." While tribute signiﬁcantly to solvent selectivity. It is important to note the authors interest seemed to lie more in emphasizing the (some- that this is very different than saying that dispersion interactions times overlooked) importance of induction effects, their results are do not contribute to overall gas/liquid partitioning or chromato- relevant to our present discussion of the relative importance of graphic retention. In fact, Snyder used n-alkanes of varying size to try to remove dispersion interactions in the formation of the SST.
The results for the 2-ketones are shown in Table 2. It is clear that However, a brief examination of the overall importance of disper- dispersion accounts for the majority of the interaction energies.
sion interactions is warranted.
For example, for 2-propanone, 71.2% of the cohesive energy arises Using regular solution theory [44,45], it can be shown that from dispersion forces. This goes up to over 90% for 2-undecanone.
dispersion interactions do not cancel when considering solvent Comparable results and trends were observed for n-alkylacetates, selectivity for gas–liquid partitioning. Speciﬁcally, when compar- n-alkyl nitriles, and 1-chloroalkanes. It should be noted that Kersten ing the selectivity for two non-polar solutes (e.g., pentane and and Poole [50] caution that Meyer's methodology is not well estab- hexane) offered by two different non-polar solvents (e.g., benzene lished and potentially overestimates the contribution of dispersion and toluene), selectivity differences between the two solvents exist.
energies to the overall energy of interaction between molecules.
According to regular solution theory, these differences arise from However, they do not explain why this is so and they acknowledge (1) differences in the molar volumes of the solutes, (2) difference in that better alternatives were not available at that time. This caution the solutes' solubility parameters, (3) differences in the product of not withstanding, it is reasonable to conclude from Meyer's work Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Table 2
Cohesive energy for a 2-ketones and the percent of dispersion, induction, and orientation forces contributing to the overall energy.
Reprinted with permission from [46]. Copyright 1966 American Chemical Society.
that dispersion interactions play a signiﬁcant role in retention, even GC phases fails because the Kovats Retention Index, upon which for polar solutes in polar systems.
the GC solvent triangles are based, does not account for interfacial As mentioned earlier in this review, Tan and Carr [42] exten- adsorption of the test solutes and n-alkane standards and because sively analyzed the effects of dispersion on retention and how these of inadequate retention of ethanol, nitromethane, and dioxane (the effects change as a function of mobile phase modiﬁer and compo- three probe solutes) on phases of low polarity. After correcting for sition. They state that the "the contribution of the presumed highly interfacial adsorption effects (see the publication for more details unfavorable cavity formation process in water is actually smaller on how they did this), the authors calculated Xe, Xn, and Xd values than thought compared to the net favorability of forming disper- according to the methodology ﬁrst described by Snyder and plotted sive interactions with the stationary phase." They then use free the data as shown in Fig. 14.
energies of methylene group transfer from the gas phase to water Using a free energy-based parameter, (+159 cal/mol) and to hexadecane (−634 cal/mol) to indicate the n, and d, SQ stands for squalane, and PH is the phase of interest, importance of dispersion interactions to the retention of solutes in they replotted the data as shown in Fig. 15 [50,51]. The phases RPLC. They also provide a thorough dissection of the linear solva- generally shift to the right compared to the plot based on P tion energy relationships (LSER) that they used to quantify changes authors attributed this to a decreased contribution from proton- in the relative importance of dispersion, dipole–dipole, and hydro- donor forces as measured by the free energy-based parameter and gen bonding interactions to overall solute retention. They consider suggested this arises either because none of the phases exam- their results in light of the amount of water and modiﬁer sorbed ined have strong proton-donor properties or because dioxane is into the stationary phase for aqueous methanol, acetonitrile, and an insensitive probe for measuring proton-donor interactions. In tetrahydrofuran mobile phases from 20 to 50% (v/v). Overall, they either case, the authors challenged the basis for the construction of stress the importance of dispersion interactions between solutes the SST as applied to GC phases.
and the stationary phase. They also examine the relative cohe-sive energy densities of the mobile and stationary phases whichcontribute to retention via the cavity formation process. Cavity for- 6.4. Further challenges to the SST – test solute selection mation processes, however, also reﬂect dispersion interactions inthat interactions between components within the mobile phase or 6.4.1. Kersten and Poole – GC within the stationary phase must be broken or rearranged in order Kersten and Poole examined the use of other probe molecules to create cavities to accommodate solutes. Different organic sol- [50]. Speciﬁcally, they commented on the use of butanol in place of vents and different compositions will clearly have different effectson the cohesive energy densities of the mobile and stationary phasethat could, depending on their magnitudes, contribute to solventselectivity.
Given the work of Meyer et al. and Tan and Carr, to clas- sify solvents, it is important to accurately account for dispersioninteractions. Failure to do so may overlook important differencesbetween solvents and their ability to interact with solutes. Thus,if the procedure used by Snyder yields only approximate cancella-tions of dispersion effects, the "excess" dispersion effects must bedistributed (in some unknown fashion) throughout the remainingthree solvent parameters in the SST. This complicates the interpre-tation of these parameters and perhaps also leads to some of theunusual groupings noted in the literature.
6.3. Further challenges to the SST – interfacial adsorption in GC Kersten and Poole [50] characterized ﬁfteen GC polymeric phases and found that the relative positions of the phases within Fig. 14. GC solvent selectivity triangle from Kersten and Poole after correcting reten-
the triangle change depending on the test solutes used to deﬁne tion indices for interfacial adsorption effects.
the apices of the triangle. They further asserted that the SST for Reprinted from [50], with permission from Elsevier.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Table 3
Effect of test probes on the Xe, Xd, and Xn values of SE-30.
Ethanol, dioxane, nitromethane Propanol, dioxane, nitromethane Butanol, dioxane, nitromethane Reprinted from [52], with permission from Elsevier.
propanol, and butanol as test probes for SE-30, they found that asthe chain length increased, Xe decreased monotonically and Xd andXn had more complex changes as shown in Table 3. More polarphases such as QF-1 and CW-20M were less affected by the changes.
The authors show that the changes in the position can be reduced by dividing the corrected retention time of the alcoholhomolog by the corrected retention time of its corresponding n-alkane. However, the authors also noted changes in positions when Fig. 15. GC solvent selectivity triangle calculated using the free energy-based
nitromethane was replaced by acetonitrile or nitropropane as the parameter, ı(G0) , to deﬁne the sides of the triangle.
polarity indicator. Normalizing for changes such as switching from Reprinted from [50], with permission from Elsevier.
nitropropane to acetonitrile would be more difﬁcult as there isnot an underlying homolog series in common as there is for then-alcohols.
ethanol, nitropropane in place of nitromethane, and 2-pentanone The success of the normalization procedure suggests that the or pyridine in place of dioxane. They provided evidence that chang- number of methylene units in the test compounds is important, ing the three probe solutes would change the position of the GC which in turn suggests that dispersion or induction effects are not phases within the triangle in an unpredictable manner. Unfortu- being completely removed by subtracting the retention index on nately, they do not actually replot the selectivity triangle based on squalane. It should be further noted that in this study, no attempt these new probes to visually demonstrate the changes in position.
was made to account for solute interfacial adsorption or inadequate Changes in position, particularly if groupings change as a result, retention of the test molecules. Kersten and Poole demonstrated would call into question the utility of the SST approach as a means that this can alter retention indices and consequently X of classifying solvents. They also perhaps reinforce the concerns of i values [50].
Some of the observed changes with increasing probe chain length West examined earlier.
may therefore be due to changes in the relative contributions ofadsorption and absorption (i.e., partitioning) to the retention of the 6.4.2. Shah, Na, and Rogers – GC probes and the n-alkanes.
Shah et al. had earlier noted the sensitivity of the position of GC phases within the triangle to the choice of test solutes [52]. They 6.4.3. Betts – GC used Klee's deﬁnition of Xi values (deﬁned earlier in this review) Betts also published a GC triangle using yet another set of probe and characterized the same six phases. Fig. 16 shows a comparison solutes [53]. Based on his work, he ultimately recommended that of the results from the two reports. In general, the agreement is three GC phases are essentially all that are required for most sep- arations (SE-30, polysiloxane; QF-1, triﬂuoropropyl; and XE-60, When butanol rather than ethanol was used as the test probe, cyanoethyl) – three that had been identiﬁed in 1969 as being among the position of the phases changed dramatically. For example, the most used phases around that time, 15 years before Betts pub- the value of Xe for SE-30 changed from 0.534 to 0.246, which lished his ﬁndings [54]. Betts' somewhat vehement response to clearly would change its grouping. By examining the series ethanol, Klee et al.'s prediction that a computerized optimization for mak-ing new mixed GC stationary phases would eventually be in place[14] was "There are already far too many; let us not mix them!"Betts also cites McReynolds, who, based on his own work, wrote"It is hoped that this data will help reduce the number of liquidphases being used" [12]. He said this because of his ﬁnding thatmany phases show similar characteristics. It would be interestingto hear Betts' thoughts on today's era of two-dimensional GC andLC separations (which in some ways can be [incorrectly] thoughtof as mixed phases of a sort) and the hundreds of commerciallyavailable LC and GC phases.
6.4.4. Cooper and Lin – RPLC Based on Snyder's selectivity triangle, Cooper and Lin [55] selected toluene, phenol, aniline, and nitrobenzene to test the rel-ative importance of proton donor, proton acceptor, and dipolecharacteristics of RPLC mobile and stationary phases. Toluene wasused as a reference compound and the slopes of plots of ln k vs.
volume fraction of organic modiﬁer obtained with toluene were Fig. 16. Selectivity triangle comparing locations of six GC stationary phases reported
subtracted from comparable slopes for the other compounds. The by Klee et al. [14] with those from Shah et al. [52] to ascertain reproducibility ofpositions within the triangle using ethanol, dioxane, and nitromethane as probe intention was to isolate just the retention of the functional groups.
solutes to determine X In some ways, this is similar to Snyder's approach of correct- e , Xd , and Xn , respectively.
Reprinted from [52], with permission from Elsevier.
ing partition coefﬁcients of solutes by subtracting the partition Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 coefﬁcient of an alkane of the same size. Unfortunately, the authors tive effects make the behavior of these two solutes different enough do not convert their ﬁndings into values that can be plotted in a so as to provide distinct chemical information.
triangle and thus the results of this study using different probesolutes cannot be readily compared to other studies using Snyder's 7. Re-evaluation of the SST using solvatochromism and
linear solvation energy relationships (LSERs)
7.1. Reevaluating the SST using solvent solvatochromic 6.4.5. Smith – RPLC The last paper we will note in this section regarding Snyder's selection of probe solutes is that of Smith [56]. In this work, prin- In 1989, Snyder participated in a reevaluation of the solvent cipal components analysis of RPLC data on eight columns with triangle [57]. This work produced three major results: three different mobile phase compositions was used to determinethe number and identity of test compounds needed to account forthe variance in retention indices using alkyl aryl ketones as stan- (1) More thermodynamically rigorous corrections for dispersion dards. Six potential test solutes were studied (aromatic analogs and entropy (cavity formation) effects produced only slight of Rohrschneider's and McReynold's standards). Smith ultimately modiﬁcations to the relative position and groupings of solvents concludes that toluene, nitrobenzene, 2-phenylethanol, and p- compared to the original SST, and the modiﬁcations that did cresol give optimal discrimination between mobile and stationary result could be rationalized chemically, phases. This is an interesting result in that four compounds were (2) The selectivity parameters (Xe, Xd, and Xn) were shown to be found to be necessary, in contrast to Snyder's suggestion that three composite values comprised of dipolar, hydrogen bond acidity, sufﬁce. It is also interesting that toluene is included in the four. This and hydrogen bond basicity effects, and suggests that dispersion and/or dipole–induced dipole interactions (3) The three original probe solutes used to develop the SST were are important in discriminating/characterizing different mobile acknowledged to be "inefﬁcient" choices in terms of their ability and stationary phases, which is consistent with Meyer et al.'s work to discriminate between solvents.
discussed above. If this is correct, then mobile or stationary phaseswith greater ability to participate in these interactions could show We will leave the interested reader to explore points 1 and 3 in greater selectivity for non-polar and polarizable compounds. This the publication and focus on the second point.
seems to be an argument against Snyder's assertion that disper- To analyze the meaning of the selectivity parameters, the sion effects are negligible in solutions of polar solvents [10]. Snyder authors plotted values of Xe, Xd, and Xn for various solvents vs. the does acknowledge that "there is no doubt that the inclusion of solvent parameters ˇ, ˛, and *, respectively. The parameters *, ˛, additional test solutes improves the ability to predict solute reten- and ˇ, are measures of solvent dipolarity/polarizability, hydrogen tion behavior and to carry out ﬁne-tuning of the solvent selectivity bond donating ability, and hydrogen bond accepting ability, respec- based on second-order effects" but doing so "appears more to con- tively [58–62]. They are derived largely from spectroscopic shifts fuse than to clarify our understanding of solvent selectivity for of aromatic compounds that are sensitive to their chemical envi- a given application." Snyder does continue on in his article to ronment and hence are sometimes referred to as solvatochromic consider X values for toluene and shows them to have little vari- parameters. Given that they are based on spectroscopic data, they ation between different solvents. One could postulate, then, that are derived from data entirely independent from that used to deﬁne in Smith's study, toluene would be the least important of the four P and Xi values. Furthermore, through judicious selection of mul- probes in terms of its contribution to the primary principal compo- tiple solvatochromic probes, the *, ˛, and ˇ scales were very nents that recreate the data set and that it is there to ‘ﬁne-tune' the carefully constructed to measure only the solvent interaction abil- model for minor effects of dispersion forces. This is not the case, ity of interest and to exclude contributions from other possible however, as shown by the principal components analysis results interactions (e.g., ˛ is a measure of just a solvent's HB donating ability with very little or no contribution from polarity or HB accept- It would be interesting to see the effects of dropping toluene ing ability). It is also worth noting that dispersion interactions from the data that was fed into the principal components analysis.
play almost no role in solvatochromism. Dipole-induced dipole Unfortunately, Smith did not perform this analysis. It is also inter- effects arising from solvent polarizability do contribute, though, esting to note the apparent redundancy of 2-phenylethanol and and dispersion interactions tend to be collinear with polarizabil- p-cresol as test probes, which suggests that resonance and induc- ity. Dipole–induced dipole interactions tend to be much smaller Table 4
Factors calculated with principal components analysis of the retention indexes of six reference compounds.
Contribution from reference standard Reprinted with permission from [56]. Copyright 1984 American Chemical Society.
a Percent of overall variance attributed to this component. Components 4–6 have been omitted because they contribute so little (<4%) to overall variance.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 in magnitude than dispersion interactions, as indicated by Meyer'swork discussed above.
Plots of Xi values for a variety of solvents vs. their corresponding *, ˛, or ˇ values are shown in Fig. 17 [57]. Assuming *, ˛, ˇ tobe ‘pure' scales in terms of measuring only a single intermolecularinteraction ability (which is known not to be case for *), if Xi valuesfor a set of solvents correlate strongly with the corresponding sol-vatochromic parameters, then the Xi values would also be said to bequite pure. However, as the authors point out, there is "disappoint-ingly little correlation of the selectivity factors with the individualsolvatochromic parameters." They note, however, that in reality,it is not the Xi values that should be correlated with the solva-tochromic parameters, but rather PXi values. Still they found littlecorrelation between parameters suggesting that the two methodsof characterizing solvents were not measuring the same attributes.
To understand better what the Snyder parameters represented, theauthors next used multi-parameter linear regressions to correlatePXi with the solvatochromic parameters *, ˛, ˇ, and ı, where ı isa term added to account for polarizability effects not incorporatedin * [63]. The correlations thus took the form PXi = SPo + s∗ + dı + a˛ + bˇ + h˛ˇ where SPo is an intercept term. The parameter ı is set equal to 0.00,0.500, or 1.00 for aliphatic, halogenated, and aromatic solvents,respectively. The results of the regression are shown in Table 5.
As the authors point out, these results indicate that all three original test solutes have appreciable dipolar interactions withsolvents as indicated by their large positive s-coefﬁcients. Further-more, dioxane and ethanol are both sensitive to solvent hydrogenbond acidity (positive a-coefﬁcients), negating the assumption thatXd is the primary measure of solvent HB donating ability in theSST. It was also concluded that the assumption that ethanol is themain probe of solvent basicity is correct as evidenced by its largeˇ-coefﬁcient compared to that for dioxane and nitromethane. Inthis way, the authors showed that (1) Xi is a composite of solvent dipolarity/polarizability, HB acidity, (2) Xd reﬂects a blend of solvent dipolarity and HB acidity, and(3) Xn mainly reﬂects dipolarity with smaller contributions from HB acidity and basicity.
The authors go on to propose that triethylamine (* = 0.14, ˛ = 0.00, ˇ = 0.71) and triﬂuoroethanol (* = 0.73, ˛ = 1.51, ˇ = 0.00)be used to probe solvent HB acidity and basicity, respectively. This Fig. 17. Plots of Snyder parameters vs. related Kamlet–Taft solvent parameters to
is based on their relatively high ˇ/* and ˛/* ratios. While the compare the similarity (or lack thereof) of solvent properties measured by each. (a) ˛-value for triﬂuoroethanol is high, a * value of 0.73 is also quite Xe vs. ˇ, (b) Xd vs. ˛, and (c) Xn vs. *.
Reprinted from [57], with permission from Elsevier.
high (given that the scales generally range from 0.00 to 1.50), suchthat it is questionable as to how much using this probe would helpin determining a pure basicity contribution to the SST free fromdipolar interactions.
Table 5
LSER coefﬁcients showing the contributions of polarity, dispersion, and hydrogen bonding effects on the PXi values of several probe solutes.
Reprinted from [57], with permission from Elsevier.
Standard deviations of the coefﬁcients are in parentheses.
a These coefﬁcients were found to be not signiﬁcantly different from zero and were omitted in the ﬁnal ﬁt.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 18. Solvatochromic parameter-based plot of properties of aliphatic solvent classes and some speciﬁc solvents (left). Further simpliﬁcation of the plot obtained by
averaging Xi values for solvents of a given type (amines, alcohols, etc.) (right).
Reprinted from [43], with permission from Elsevier.
7.2. Solvatochromic SST for solvents explain the exact nature of the dependence of the original SST onprobe solute selection. The use of solvatochromic parameters to As an extension of the ideas presented in the article just dis- reconstruct the SST was also new.
cussed, Snyder et al. reconstructed the SST using the Kamlet–Taftsolvatochromic parameters to deﬁne the apices [43]. To do so, each 7.3. Solvatochromic SST and practical RPLC considerations solvent parameter (*, ˛, ˇ) was normalized to the sum ( It is worth extending our discussion of Snyder et al.'s exami- the three parameters for each individual solvent. The normalized nation of the SST as it relates to solvent selection in RPLC [43]. As parameters were used as the apices of the triangle.
presented earlier, the SST was used as the basis for many optimiza- In order to facilitate the comparison between the solva- tion schemes. However, while the SST was proposed as a guide to tochromically based triangle and Snyder's original SST, the authors aid in solvent selection, it does not provide guidelines regarding averaged Xi values for solvents within a class (e.g., amines, alcohols, the effect of increasing the percent water in each of the solvents on etc.). They also only compared aliphatic solvents, largely because chromatographic selectivity. Along those lines, the authors noted all but one of the aromatic solvents studied had ˛ = 0.00 and thus that the "SST approach assumes that solvent strength can be varied they clustered along the right vertex of the triangle. The original and (by varying the percent water in RP-HPLC) without changing selec- ‘new' plot, thus simpliﬁed, are shown in Fig. 18 [43]. The authors tivity" (italics ours). But water is certainly not a passive diluent, as the authors attest by pointing to changes in the *, ˛, ˇ values of "the relative positioning of different solvents. .is similar in that solvents modiﬁed with varying amounts of water [30,31,64,65]. We solvents which are more basic, acidic, or dipolar in [the original] agree with their statements that the "SST approach to adjusting sol- are also more basic, acidic, or dipolar [in the new plot]. A further vent strength and selectivity in RP-HPLC is overly simpliﬁed" and examination. .however, shows that solvents of similar acidity that "it is all but impossible to vary the mobile phase strength via or basicity are better grouped in the solvatochromic approach.
a change in the water content without also changing some other Thus, amines and ethers show up as distinctly basic, as com- signiﬁcant solvent-selectivity property" [43]. Speciﬁcally, they go pared to the alcohols in [the original plot]. The alcohols, glycols, on to note that previous studies show that, with respect to selec- formamide, carboxylic acids, water, and chloroform show up tivity, water simultaneously affects the mobile phase cohesivity as acidic solvents in [the new plot]. The acidity of these latter (i.e., the ease of cavity formation to accommodate solutes), polarity, solvents seems inadequately expressed in [the original]." and HB acidity, with only minor changes in basicity. They suggest,therefore, that for RPLC purposes, the SST should be reconstructed They go on to suggest that these problems (and a few oth- using surface tension, or some other cohesivity-related property, ers) in the original SST can likely be attributed to the fact that polarity, and hydrogen bond acidity to deﬁne the apices, thus elim- nitromethane, ethanol, and dioxane do not provide pure mea- inating hydrogen bond basicity. The fact that the mobile phase sures of polarity, basicity, and acidity, whereas the solvatochromic also modiﬁes the stationary phase properties is also noted as a parameters were designed to do just that. Furthermore, the solva- complication in predicting selectivity changes between different tochromic parameters are averages obtained with several probes solvents and solvent compositions. These effects were comprehen- for the determination of each *, ˛, and ˇ value. This reduces some sively explored by Tan and Carr [42]. Using linear solvation energy of the probe-speciﬁc effects that are inherently embedded in the relationships, they demonstrate changes in the relative contribu- construction of the SST.
tions to solute retention of cavity formation, dispersion, dipolarity, As a ﬁnal, and rather eloquent, explication of why it is that and hydrogen bonding interactions as a function of mobile phase the original three probes represent blends of interactions, theauthors provide their solvatochromic parameters, reproduced herein Table 6 [57]. These values make it clear that all three solutes are polar and that dioxane and ethanol are both good hydrogen bond *, ˛, and ˇ values of Snyder's original test probes showing that they participate in acceptors (high ˇ values). Thus, any parameters derived from this a blend of intermolecular interactions and do so to varying extents.
triad of solutes will necessarily represent blends of interactions.
Given all of the challenges that had come before this work, the solute-dependent nature of the original SST was not a novel reve- lation (as the authors acknowledge via their citations). What was new, however, was the use of the solvatochromic parameters to Reprinted from [57], with permission from Elsevier.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 modiﬁer (methanol, tetrahydrofuran, and acetonitrile) and com-position. They review multiple studies of sorption of water andorganic modiﬁer into the stationary phase [66–75] and interprettheir ﬁndings in light of the modiﬁcations of the stationary phaseby sorbed water and organic solvent. Snyder et al. [43] acknowl-edge that if these changes were incorporated into an LC-speciﬁctriangle, the solvent classiﬁcations/groupings would change, butthey defend the overall SST approach as a useful one in a qualitativesense.
7.4. Solvatochromic SST for GC Li et al. extended the considerations of solvatochromically derived LSERs to include characterizing GC phases [76]. Theirapproach is based on the LSER equation where SP is the logarithm of the speciﬁc retention volume (Vog),partition coefﬁcient (K), or retention factor (k) for a compound(denoted by the number ‘2') on a given phase. Log L16 is the solutegas-to-n-hexadecane partition coefﬁcient. The parameters ∗,c, ˛c , and ˇc are measures of a solute's dipolarity/polarizability, hydro- Fig. 19. Classiﬁcation of GC stationary phases using a triangle based on LSERs. See
gen bond acidity, and hydrogen bond basicity, respectively [77,78].
reference for groupings.
The ı2 parameter is meant to account for polarizability effects not Reprinted with permission from [76]. Copyright 1992 American Chemical Society.
included in ∗,c. SP o is a solute-independent constant speciﬁc to the stationary phase being studied, and l, s, a, b, and d are column- than just three. The second is that each of the probe solute's sol- related parameters determined by regression of SP measured for vatochromic parameters are more carefully deﬁned to isolate the a large number of solutes (dozens if not hundreds) against their speciﬁc intermolecular interactions being represented, as opposed corresponding ∗,c, ˛c , ˇc , and ı 2 values. The important aspect to Snyder's three probe system which was shown earlier to have is that the coefﬁcients quantify the ability of the stationary phase blends of interactions represented by each probe. This study is to interact with solutes through various intermolecular forces. For also interesting because of its redeﬁnition of the apices to include example, the ˛c parameter reﬂects the solutes' abilities to donate dispersion effects (embedded in the l log16 term) in favor of HB hydrogen bonds. Therefore, a large, positive a-coefﬁcient indicates donating effects, which seems an imminently reasonable substi- that the stationary phase strongly retains HB donors and is there- tution based on the actual intermolecular interactions that govern fore itself a strong HB acceptor (i.e., the phase is basic). Thus, the selectivity in gas chromatography.
coefﬁcient reﬂects the complementary property of the solute.
The authors selected 53 representative GC phases from data 7.5. An important note about LSER ratios sets collected by McReynolds [13], Poole and co-workers [79], andCarr and co-workers [77,80] and performed LSER analyses accord- While Li, Zhang, and Carr based their solvatochromic GC trian- ing to the equation above. Principal components analysis showed gle on absolute values of the LSER coefﬁcients, later work from the that three components account for over 98% of the variance in the same research group indicates that for determining selectivity, the Poole and McReynolds data sets (results for Carr's data set were ratios of the LSER coefﬁcients are the distinguishing parameters not provided). Based on this and the LSER results, it was con- [81]. This can be shown by considering the correlation of log k val- cluded that three parameters could be used to characterize each ues with two independent solute properties (Xi and Yi) as shown in GC phase. Because the l, s, and a coefﬁcients (dispersion/cavity for- the equations below (LSERs generally use four or ﬁve parameters, mation, dipolarity/polarizability, and HB acidity) have the largest but considering two here sufﬁces to illustrate the point): LSER coefﬁcients, those coefﬁcients were selected to deﬁne theapices of a solvatochromically based GC–SST. There are very few log k1,i = a1 + b1Xi + c1Yi GC phases that are even slightly good hydrogen bond donors, so the b-coefﬁcients are always quite small or statistically insigniﬁcant.
2,i = a2 + b2Xi + c2Yi As in the earlier solvatochromic study, the coefﬁcients had to be The subscripts 1 and 2 refer to two different chromatographic normalized in order to be plotted in a triangle. Three parameters systems (e.g., two different stationary phases, mobile phases, or sta- were thus deﬁned: tionary/mobile phase combinations). Combining the two equationsyields Note that if the ratio c1/b1 = c2/b2 then the retention on one phase correlates perfectly with retention on the other, regardless of what solutes are used or their properties. Zhao and Carr state that in this The resulting triangle plot is shown in Fig. 19 [76]. The authors case, there is no difference in the "effective selectivity" of the two comment that very few phases are located in the HB acceptor systems. By "effective selectivity" they mean differences that lead corner owing to the fact that few columns are very basic while to elution order changes and differential changes in band spacing, as being of low polarity. They also reiterate two advantages of an opposed to merely spreading out peaks a little more in one system LSER-based triangle scheme for phase classiﬁcation. The ﬁrst is compared to another. If c1/b1 / = c2/b2, then retention on the two that LSERs are determined using dozens of probe solutes rather phases might not be correlated and instead depends on the solute Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 properties present in the analyte mixture. In this case, if both Xiand Yi for the solutes make substantial contributions to retention,then "effective" or useful changes in selectivity could result fromchanging from one system to the other. So the key to obtaininguseful selectivity is to have ratios, not necessarily absolute mag-nitudes, of LSER coefﬁcients that are different. For this reason, theGC selectivity triangle discussed previously would have been bet-ter presented if ratios of LSER coefﬁcients had been used to deﬁnethe apices rather than absolute magnitudes.
8. Recent uses of selectivity triangles – MEKC, RPLC, and
NPLC
8.1. MEKC selectivity triangles based on LSERs Based on all of the work over the years that has been summa- rized above, Fu and Khaledi have recently characterized pseudophases used in electrokinetic chromatography (EKC) [82,83]. Thephases included elution buffers modiﬁed with micelles, polymers, Fig. 20. Micellar selectivity triangle based on LSERs. See reference for groupings.
vesicles, liposomes, mixed micelles, polymer/surfactant mixtures, Reprinted from [82], with permission from Elsevier.
and organically modiﬁed pseudo phases. This is the ﬁrst report thatthe present authors are aware of in which an SST approach wasapplied to micellar and related systems.
As a critical test of the methodology and the reproducibility of Their triangle is ultimately based on LSERs of the form using LSERs in this manner, Fu and Khaledi collected fourteen dif-ferent literature reports of LSERs for sodium dodecyl sulfate (SDS) and plotted them in a triangle shown in Fig. 21. It is reassuring thatthey generally cluster together. Reasons that a few of the results where V, B, A, S, and E are measures of a solute's volume, HB basic- are outliers can be offered based on differences in experimental ity, HB acidity, dipolarity/polarizability, and excess polarizability, respectively [84,85]. The values of c, v, b, a, s, and e are determined Returning our attention to Fig. 20, the authors identiﬁed four by linear regression analysis and were either taken from literature different groupings of systems labeled A, B, C, and D. As with other reports or measured by the authors.
selectivity triangles, the suggestion is that if a system in one group- The deﬁnition of the apices of their triangle is somewhat more ing does not achieve the desired separation, then switching to complex than others discussed in this review. First, the authors another system within the same group is unlikely to produce dra- calculated the ratio of LSER coefﬁcients as suggested by the Carr matic changes in elution order or selectivity. Rather, it would be publication discussed above [81]. They choose to normalize to the better to change to a system in a different group that might have v-coefﬁcient, which is commonly done because the v-coefﬁcient is different blends of intermolecular interactions and therefore might often one of the largest in LSERs, particularly those involving solute offer different selectivity.
transfer into or out of aqueous phases. The symbol Ii is given to eachpossible ratio (a/v, b/v, s/v, e/v), where the subscript ‘i' representsany one of the individual ratios. Next, the I 8.1.1. Analysis of the MEKC selectivity triangle i values are converted to As with the original Snyder triangle, some challenges can be made to this classiﬁcation scheme. First, the vertices are labeled with "polarity", "basicity", and "acidity" as if they are absolute mea- where the ranges of Ihigh and Ilow were selected to incorporate (butnot equal) the high and low values for each ratio for the 74 sys-tems studied. For example, Ihigh = −1.50 and Ilow = 0.00 for b/v, eventhough for the 74 systems, the actual lowest value was −1.38 andthe highest was −0.23. While the actual Ihigh and Ilow values wereadjusted for each ratio being considered, the difference betweenthem (i.e., the range) was kept constant at 1.50. Deﬁning Ui in thisway provided quantities that were all positive (unlike LSER coefﬁ-cients which can be positive or negative) and which ranged from0.00 to 1.00.
Next, in a manner similar to that in Brown's original work, the Ui values were normalized according to such that Xa + Xb + Xc = 1.00. These three Xi values then served asthe apices of the micellar selectivity triangle (MST). With four LSERcoefﬁcient ratios, there are obviously several different triads thatcan be used to deﬁne a triangle and the authors explored theseoptions. They ultimately recommended one based on Xb + Xs + Xa.
Fig. 21. Micellar selectivity triangle showing data points based on fourteen litera-
Using this scheme, the 74 systems were plotted as shown in Fig. 20 ture reports for sodium dodecyl sulfate LSERs.
Reprinted from [82], with permission from Elsevier.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 23. Plot of b/v vs. b to show the inﬂuence of v-coefﬁcients on the interpretation
of pseudophase properties as deﬁned by I-values in the development of the MST.
Fig. 22. Plot presented to show a poor correlation between Xb and v-coefﬁcients,
ascending order. This suggests that the smaller v-coefﬁcients (per- suggesting that the X scales in the MST are not inﬂuenced by differences in haps arising from easier cavity formation or weaker solute/micelle v-coefﬁcients for the various pseudophases.
Reprinted from [82], with permission from Elsevier.
dispersion interactions in these micelles compared to others) areleading to the high magnitudes of b/v ratios. Thus, it is perhaps notan acidity effect but rather a different effect that places them inthe group in which they reside within the triangle. This suggestion sures, whereas in reality they are quite complex parameters. Their is supported by arbitrarily replacing the actual v-coefﬁcients for complexity can be recognized by ﬁrst considering that they are these systems with the average v-coefﬁcient calculated using all of ratios of LSER coefﬁcients. Then, they are normalized to an arbi- the systems. If the plot is remade (Fig. 24), it is clear that the eight trary high and low value, and then get renormalized to the sum ‘outliers' ﬁt into the general correlation. So the apparent enhanced of three such normalized parameters. This means that they are magnitude of the AGENT and Elvacite 2669 systems (in terms of not truly direct measures of any single selectivity characteristic of larger negative b/v ratios) is more a result of low v-coefﬁcients.
the system. For example, when the authors state that "Group B is Similarly, the apparently smaller-than-expected magnitude of the mainly comprised of ﬂuorinated micelles and could be considered b/v ratio of octanol/water partitioning is a result of a larger-than- the strongest hydrogen bond donor and weakest hydrogen bond average v-coefﬁcient, as demonstrated by replacing its v-coefﬁcient acceptor among all the micelle systems" or "In general, the compo- with the average and replotting it as shown in Fig. 24. These con- nents in group C are slightly stronger hydrogen bond acceptors and cerns do not negate the use of the MST, but they complicate the weaker hydrogen bond donors than those in group A", these state- chemical understanding of why the systems fall where they do ments would only be true if the v-coefﬁcients for all of the systems within the triangle.
were the same. However, the v-coefﬁcients in their collection vary In terms of absolute strengths of interactions, it is useful to look from 1.49 to 3.78 (excluding the value of 3.94 for octanol/water par- at the interpretations of LSERs. In general, the solute partitioning titioning which was included in their study as a bulk phase model of is deﬁned as the transfer of the solute from the aqueous phase into micelle/water partitioning). This is a relatively large range for LSER the pseudo phase. Thus, negative coefﬁcients indicate the solutes coefﬁcients and quite comparable to the overall range for the b- partition less as their solute parameters increase. For example, a coefﬁcients in this study (−0.47 to −3.86). Even if the v-coefﬁcients negative b-coefﬁcient indicates that the aqueous phase is a stronger were the same, it is difﬁcult to make these statements because Xi is hydrogen bond donor than is the pseudo phase (which typically a relative measure of the property under consideration compared makes sense given the ability of water to donate hydrogen bonds).
to the sum of three different properties. Thus, all that really can The magnitude of the coefﬁcient indicates the degree to which this be said, for instance, is that the contribution of the acidity/cavity is true. The larger the magnitude, the weaker the hydrogen bond formation ratio compared to the overall sum of basicity/cavity for- donating ability of the pseudo phase. A coefﬁcient of zero indicates mation, acidity/cavity formation, and polarity/cavity formation is that the pseudo phase is just as strong a donor as the aqueous phase, highest for systems in group B. Even this, however, is an oversim- and a positive coefﬁcient indicates that the pseudo phase is a better pliﬁcation because the solute parameter V (solute size) models bothcavity formation (endoergic) and dispersion (exoergic) effects. Sothe interpretation of the v-coefﬁcient is itself not simple. Thus, atbest, the descriptors along the sides of the triangle are oversimpli-ﬁcations and serve, perhaps, as ﬁrst approximations or convenientlabels of what are quite complex measures of the systems'characteristics.
To demonstrate that the X scales are not inﬂuenced by the magnitudes of the v-coefﬁcients in the manner suggested in theparagraph above, Fu and Khaledi show a plot of Xb vs. v, which hasgenerally scattered data for the 74 systems (see Fig. 22) [82].
We have developed the related plot of b/v vs. b shown in Fig. 23.
If all of the v-coefﬁcients were identical, such a plot would resultin a straight line. However, it is clear that several systems fall wellbelow the general correlation. The outliers correspond to the sevenAGENT polymeric micelles and Elvacite 2669. These eight systems Fig. 24. Same plot as in the previous graph except that the v-coefﬁcients for the
have the six lowest v-coefﬁcients of all 74 systems and the other two AGENT surfactants, Elvacite 2669, and octanol–water have been replaced with the are numbers nine and twelve when all 74 v-coefﬁcients are listed in average v-coefﬁcient for the set of 74 pseduophases.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 25. Plots of Xi vs. i to compare the triangle parameter (Xi) to the LSER (i) parameter and the complications that can arise when interpreting Xi values. (a) Xb vs. b, (b) Xa
vs. a, (c) Xs vs. s.
HB donor than the aqueous phase. When one lists the b-coefﬁcients they actually interact more strongly with polar solutes than does for all of the systems from smallest negative (i.e., strongest donor) water (or more precisely, the aqueous phases used in these studies).
to largest negative (i.e., weakest donor) the perﬂuorinated surfac- Thus, it appears that the normalization process is not accurately tants are numbers 1–5 and 11 in a list of all of the systems. Thus, simultaneously reﬂecting all of the properties of these phases.
on the absolute scale, they are the strongest HB donors just as they As a ﬁnal illustration of the problem of interpreting the axes, are in the triangle, so the normalization process does not appear to when the authors plot Xb + Xs + Xe (instead of Xb + Xs + Xa) the per- distort their position with regards to their HB donor strength. How- ﬂuoro surfactants switch from having the lowest ‘dipolarity' values ever, the AGENT pseudo phases are seen as some of the weakest to the highest (ﬁgure not shown).
HB acids on the triangle, which is inconsistent with their absolute Of course, it must be noted that some of the above conclusions values when compared to all of the other systems.
about the MST are drawn based on a consideration of the absolute It is possible to argue that the normalization of b/v values to values, and not ratios of LSER coefﬁcients which, as pointed about high and low values and then to the sum of Ui values as dictated above, are the more critical parameters to consider when interested by the methodology removes the effect of the small v-coefﬁcients in selectivity differences between systems. Nevertheless, while they such that the Xi values that are ultimately plotted in the triangle do not negate the utility of the triangle, they do show that the state- accurately reﬂect the relative intermolecular interaction strengths ments made about the various systems and the labeling of the sides of the mobile phases. Fig. 25a–c shows plots of Xi vs. I for i = b, a, of the triangle are at best oversimpliﬁcations.
and s. These plots make it clear that the way in which the apicesof the triangle are deﬁned, combined with the magnitude of the 8.2. RPLC column selectivity triangle based on the hydrophobic v-coefﬁcients, can produce over- or underestimated strengths of subtraction model speciﬁc classes of phases. For example, the AGENT surfactants haveunderestimated Xb and Xs values given their absolute magnitudes Quite recently, Zhang and Carr [86] published multiple trian- for the corresponding b- and s-coefﬁcients. These underestimated gles based on the Snyder–Dolan hydrophobic subtraction model of Xb and Xs values are offset by overestimated Xa values. These values column selectivity [87] which takes the form do not result because of enhanced acidity and polarity of these sur- factants, but rather because of their small v-coefﬁcients relative to = H − S∗ + ˇA + ˛A + C most systems. The fact that their basicity (X a) is overestimated is a mathematical artifact that arises from the requirement for the sum where the column parameters H, S*, A, B, and C are obtained of all X values to equal 1.00. If some parameters are underestimated, via multiparameter linear least squares regression of log(ki/kEB) then others will necessarily be overestimated.
against the known solute descriptors , , ˛, ˇ, and for a To further complicate the analysis of the triangles, we note that set of solutes, i, analyzed with a given mobile phase and sta- group B is seen to have the lowest dipolarity according to the labels tionary phase for different columns. H, S*, A, B, and C provide on the triangle. This contradicts what is observed based on absolute measures of solute–column interactions. Speciﬁcally, they rep- values of the s-coefﬁcients. In fact, the perﬂuoro surfactants are the resent hydrophobicity, steric resistance, HB acidity, HB basicity, only pseudo phases that have positive s-coefﬁcients, indicating that and cation-exchange activity, respectively, of the mobile/stationary Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 26. RPLC selectivity triangles based on the Snyder–Dolan hydrophobic subtraction model for 366 stationary phases and a single mobile phase with a particular weighting
factor (see reference for details). (a) S*–B–C triangle, (b) S*–A–C triangle, (c) A–B–C triangle, (d) S*–A–B triangle.
Reprinted from [86], with permission from Elsevier.
phase combination being studied. Data for sixteen solutes analyzed shown in Fig. 26. These triangles used a weighting factor deﬁned on 366 commercial RPLC phases were collected and analyzed using in such as way as to yield the same quantitative effect on phase the hydrophobic subtraction model. The resulting H, S*, A, B, and C selectivity (deﬁned as the standard error in a log k vs. log k plot for values were used to construct selectivity triangles according to the retention of sixteen solutes on the different phases) for an equiva- lent numerical change in two different normalized phase properties First, ratios of the coefﬁcients were calculated (in accord with (see the original reference for more details). A brief examination the earlier discussion which showed that it is the ratios, not the of the triangles developed using this weighting shows that the C absolute values of coefﬁcients, that must be compared in order to parameter (ionized silanol effects) dominates the three triangles in compare the selectivities of two different chromatographic sys- which it appears. The effect is to cluster all but the most dissimilar tems). The authors selected H as the parameter to which other phases. Such clustering makes it impractical to use the triangles to coefﬁcients were normalized.
select phases of differing properties, or to distinguish one group The authors then deﬁned a parameter Xi as of columns from another as is usually done with triangles. Theauthors thus sought a different weighting scheme, using instead Xi = (I − Imin)i where I = S*/H, A/H, B/H, or C/H and i is a weighting factor. Todevelop a triangle, three j values were deﬁned as Such that Xi becomes where j = S*, B, or C.
Clearly, with four different I-ratios, four different sets of three I-values are possible. Thus, four different triangles were plotted as Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 27. RPLC selectivity triangles based on the Snyder–Dolan hydrophobic subtraction model for 366 stationary phases and a single mobile phase with a different weighting
factor compared to the previous plot (see reference for details). (a) S*–B–C triangle, (b) S*–A–C triangle, (c) A–B–C triangle, (d) S*–A–B triangle.
Reprinted from [86], with permission from Elsevier.
which is akin to one of the steps in the development of the micellar they may not be truly needed as they do not add to our ability selectivity triangle (MST) of Fu and Khaledi discussed elsewhere in to achieve separations. Their second, and perhaps more impor- this review.
tant conclusion, is that commercially available stationary phases The use of this weighting factor resulted in the four selectivity are not exploring all possible blends of intermolecular interactions triangles shown in Fig. 27. With these triangles, the authors ﬁnd that and thus not providing a full range of selectivities. It is interesting to type-B silicas derivatized with alkyl chains are generally grouped note that this is the same conclusion that Brown reached 50 years together in the center. Phases derivatized with cyano, phenyl, ﬂu- ago, and which Betts reiterated in 1986, regarding GC stationary oro, or polar embedded groups and those based on type-A silicas phases as discussed above.
generally show larger differences in coefﬁcients and fall outside ofthe central cluster. All phases of a given chemical compositional 8.2.1. Analysis of the RPLC selectivity triangle class certainly do not fall in the same region of the triangle.
Given the similarity of this approach based on the hydropho- The authors also comment on some surprising ﬁndings. For bic subtraction model with that of Fu and Khaledi's based on LSERs, example, the three chemically different columns (ACE AQ – a polar many of the same potential advantages and disadvantages exist. For embedded phase; Betasil Phenyl-hexyl – a phenyl phase, and Bond- example, both approaches rely on entire sets of solutes, as opposed clone C18 – a type A alkyl silica) are near each other in the triangle.
to just three probe solutes, to deﬁne the apices of the triangle. This This suggests that their selectivities are comparable, as was veriﬁed increases the probability that the results are more broadly repre- by high correlation coefﬁcients and small standard error values for sentative and would apply to a broad range of solutes.
regressions of log k on one column vs. log k on another for the set A disadvantage is that to create the plots, one parameter of the of sixteen variegated test solutes.
model is ignored. Thus, two phases that are identical in three of the Zhang and Carr make two important points about the phases four parameters may appear to have similar selectivities in one of they studied, stating that "a huge fraction of the available space [in the triangles. Therefore, use of any one triangle may be blind to a the triangles] is under populated and certain regions are extremely major difference in selectivity of two phases which is very evident over populated" [86]. So their ﬁrst conclusion is that on one hand, in a different triangle. This is particularly important if the solute many of the phases are quite comparable to one another, meaning set includes compounds that differ in the property that is comple- Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 28. Illustration of solute and solvent general adsorption compared to localization. (a) Non-localized retention of chlorobenzene on silica with dichloromethane as mobile
phase; (b) localized retention of phenol, with tetrahydrofuran as mobile phase.
Reprinted with permission from [88].
mentary to the one that is not plotted (i.e., solute HB acidity paired 8.3. NPLC selectivity triangle with considerations of system HB basicity). The limitation of threeparameters is overcome by creating four different triangles, but the In addition to the recent uses of triangles in MEKC and RPLC different plots can lead to different conclusions regarding similar detailed above, Snyder has recently reviewed solvent selectivity and different phases. So the need for multiple plots can compli- and its applications to NPLC [88]. The ﬁrst part of the review makes cate the use of the selectivity triangles for selecting orthogonal (or it clear that the main mechanisms of solute retention on polar sur- similar replacement) phases.
faces – the work focuses on alumina and silica adsorbents – are (1) Lastly, as pointed about above, the use of normalized parameters non-localized adsorption to the surface via displacement of mobile complicates the chemical interpretation of the parameters. Zhang phase molecules and (2) localized interactions with the formation and Carr are careful in their manuscript to avoid labeling the sides of speciﬁc interactions between analytes and the stationary phase.
of the triangles with absolute descriptors as Fu and Khaledi did. In The former predominate for non-polar solutes and the latter for fact, they explicitly recognize that the normalization complicates compounds containing polar function groups. Both types of inter- interpretations of the derived parameters. This does not preclude actions are depicted in Fig. 28.
the use of the triangles in a practical sense but does limit the degree Snyder focuses on the effects of the "B-solvent" – the more polar to which chemical meaning can be ascribed to conclusions based solvent in a mixed mobile phase. The A-solvent is typically some- on them regarding similar and different phases.
thing like n-pentane or cyclohexane. He points out that if a polar, Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 (9) 1-naphthaldehyde; (10) 1,5-dinitronaphthalene; and (11)1-acetonaphthalene.
The ﬁrst plot in this ﬁgure compares the two non-localizing B- solvents benzene and carbon tetrachloride. The log k values arehighly correlated, meaning that the retention mechanisms withboth phases are essentially identical. When a localizing B-solvent(acetonitrile) is compared to a non-localizing one (benzene), thecorrelation is poor, indicating different interactions are governingretention, creating potential selectivity differences with the differ-ent mobile phases. In these plots, it is clear that polar, localizingsolutes such as 2-methoxynaphthalene, 2-nitronaphthalene, and1-naphthaldehyde are each affected differently by the presence ofacetonitrile in the mobile phase.
To further understand and differentiate the effects of differ- ent B-solvents, Snyder correlates ı log k values from one – plotwith ı log k values from a second – plot for the eleven solutesshown in Fig. 29. The squares of the correlation coefﬁcients forthese ı log k vs. ı log k plots are shown in Table 7 (adapted from[89]). To aid in understanding the different results, Snyder uses thesolvatochromic selectivity triangle shown in Fig. 30a to differenti-ate highly basic solvents (top shaded portion of the triangle) fromweakly and non-basic solvents (those outside the top shaded por-tion). The speciﬁc B-solvents studied and their relative basicitiesaccording to the deﬁnitions used to establish the solvent triangleare shown in Fig. 30b, as are their average r2 values from the ı log kvs. ı log k correlations.
It is clear from these results that those solvents classiﬁed as non- or weakly basic (e.g., nitromethane and acetonitrile) producethe strongest correlations whereas the strongly basic solvents (tri-ethylamine, pyridine, ethyl ether, THF) have the lowest correlationcoefﬁcients. It is also clear from the data in the table that cor-relations between two non-basic solvents (upper left quadrant)produce stronger correlations than those between two basic sol-vents (lower right quadrant). Furthermore, correlations betweena non-basic and basic solvent (upper right quadrant) are weakerthan those between two non-basic solvents (upper left quadrant).
All of this indicates that the basic solvents have some additionalmechanism (or mechanisms) of interacting with solutes and/orthe stationary phase that creates additional likelihood for selec-tivity differences to exist between them. Snyder goes on to offerevidence that part of those selectivity differences relates to theability of those solvents to increase retention for proton-donatingsolutes, with the basic solvents increasing retention more than Fig. 29. Comparison of solvent-type selectivity for two equal-strength mobile
non-basic solvents. This arises because the basic solvents are con- phases; (a) non-localizing B-solvents (benzene and carbon tetrachloride), (b) one centrated on the stationary phase surface. These solvent molecules localizing B-solvent (acetonitrile). Alumina as adsorbent. See text for solutes and will preferentially interact with and increase the retention of donor Reprinted with permission from [88].
The practical upshot to all of these studies is that they provide guidance for optimizing NPLC separations. As detailed earlier in this localizing solvent, like tetrahydrofuran (THF) is replaced with a review, seven ‘training' chromatograms are used in a simplex opti- less polar one, like CH2Cl2, polar solutes will experience decreased mization scheme when optimizing three parameters. An isocratic competition for localized interactions with the surface, leading optimization scheme related to the use of basic localizing, non- to preferential retention of polar solutes compared to nonpolar basic, and non-basic localizing solvents in mobile phases of equal solutes and hence to a change in the selectivity of the separation.
solvent strength is shown in Fig. 31 (see original publication for In order to better understand the effects of the nature of the more details). Chromatograms obtained using some of the ‘training' B-solvent on selectivity, Snyder ﬁrst deﬁnes a solute-speciﬁc mobile phases are shown in Fig. 32a–c and the optimized chro- property, ı log k. ı log k values are derived by correlations of log k matogram is shown in Fig. 32d. The training chromatograms show values obtained using one mobile phase vs. log k values obtained multiple overlapping peaks and considerably different selectivi- using a second mobile phase with a different B-solvent (so-called ties for some solutes. By combining non-basic, basic, and localizing – plots). Such plots are illustrated in Fig. 29 for eleven solutes.
solvents, a minimum resolution of 1.3 was obtained for all com- The ı log k parameter is also shown in the ﬁgure. The mobile phases ponents. Comparing chromatograms b and c and the resulting are adjusted such that their overall solvent strengths, as measured chromatogram in d shows the profound effect that the addition by the solvent strength parameter, ε, are comparable. The solutes of ACN and CH2Cl2 to the mobile phase in (c) has on selectivity for are (1) 2-methoxynahthalene; (2) 1,7-dimethoxyaniline; (3) 1- solute pairs 6 + 10, 4 + 11, and 8 + 9 (an unfavorable inﬂuence for the nitronaphthalene; (4) 2-chloroquinoline; (5) 1-methylnaphthoate; Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Table 7
Squares of correlation coefﬁcients for ı log k values from one – plot correlated with ı log k values from a second – plot based on eleven solutes listed in the text studied
in nine solvents.
Dimethylsulfoxide DMSO Tetrahydrofuran THF Reprinted from [89], with permission from Elsevier.
While much of the data upon which Snyder's review rests was 9. Future directions in comparing selectivity
obtained many years ago, the creation of and subsequent develop-ments of the triangle classiﬁcation system have helped provide a 9.1. A unifying method for comparing chromatographic more complete understanding of the retention mechanism in NPLC and continues to serve as a guide for selecting initial chromato-graphic conditions in optimization schemes.
As suggested in Section 1, new methods for determining selec- tivity differences between chromatographic systems may helpovercome some of the limitations of triangle schemes that wehave described throughout this review. For example, Ishihama andAsakawa constructed vectors in ﬁve-dimensional space based onLSER coefﬁcients. They used the angle between vectors to assess thesimilarity of two chromatographic systems [90]. Instead of usingthe angle between two vectors, Abraham and Martins used thedistance between vectors as the metric for comparing two sys-tems [91]. Lázaro et al. also used the distance between vectors,but only after normalizing the vectors to be the same length [92].
Fuguet et al. used principle component analysis of LSER coefﬁcientsfor pseudostationary phases in electrokinetic chromatography,along with radial distribution plots, to assess selectivity differ-ences between the phases [93]. Principle components analysis ofmultiple column parameters such as surface coverage, hydropho-bic selectivity, shape selectivity, hydrogen bonding capacity and Fig. 30. Solvent-type selectivity as a function of the hydrogen-bond (H-B) basicity of
Fig. 31. Optimization scheme for NPLC using non-localizing, basic-localizing,
the B-solvent. (a) The solvent-selectivity triangle adapted from Ref. [88]; (b) solvent- and non-basic localizing B-solvents with A-solvents such as pentane, hexane, or type selectivity as a function of B-solvent H-B basicity.
dichloromethane for ε0 > 0.30.
Reprinted with permission from [88].
Reprinted with permission from [88].
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Fig. 33. Depiction of the selectivity differences between the surface chemistries of
packings (C18, RP18 with an embedded polar group, and phenyl) and the organic
mobile phases methanol and acetonitrile. Light grey values represent ammonium
formate (pH 3). The values on each bar are the measured selectivity differences. Note
that the largest selectivity differences are found along the diagonal lines. Shown
are the selectivity differences between the packing with an embedded polar group
with acetonitrile as the organic modiﬁer and the phenyl and the C18 column with
methanol as the organic modiﬁer.
Reprinted with permission from [96].
largest differences in selectivity (i.e., those most poorly correlated).
Snyder et al. [96] point out that this method requires adjustment ofthe solute retention times such that they span comparable rangesand is only rigorously valid if all of the system variables are indepen-dent. Nevertheless, the presentation of this work was compellingand the approach offers an interesting method for comparing sys-tem selectivities.
We recently presented a 3D visualization cube to visually detect similarities and differences between separation systems [97]. Ourmethod is based on the correlation of LSER coefﬁcients. Exam-ples of such correlations are shown in Fig. 34, which comparessodium dodecylsulfate with sodium tetradecylsulfate (STS) andwith lithium perﬂuorooctanesulfonate (LiPFOS). In these analyses,as in Fu and Khaledi's [82] and Zhang and Carr's work [86], all of theLSER coefﬁcients are ratioed to the v-coefﬁcient before the correla-tion is performed. Clearly, SDS and STS correlate strongly, while SDS Fig. 32. Examples of the application of the scheme in the previous ﬁgure for the
selection of an optimum mobile phase. Conditions: 150 × 4.6 Zorbax-SIL column;
mobile phases shown in the ﬁgure (50% water-saturated). See original publication
for details of chromatogram recreation based on retention data.
Reprinted with permission from [88].
ion-exchange capacity at pH 2.7 and 7.6 was used by Euerby andPetersson to analyze and easily visualize the similarities and differ-ences between hundreds of RPLC columns [94]. Neue et al. [95,96]recently presented a graphical method for quantifying and visual-izing selectivity differences between chromatographic systems ofvarying pH, eluent type, and stationary phase. Correlations of gra-dient retention times for the same solutes on two different systemsdiffering in one variable (pH, eluent, or stationary phase) are usedto determine s-values, deﬁned as where r2 is the square of the correlation coefﬁcient. To visualize thedata, prisms are constructed (see Fig. 33) in which the s-value thatcorrelates the two systems are used as tie-lines. In this example, dif-ferences in stationary phase type (C18, RP18 with a polar embeddedgroup, and a phenyl column) are compared, along with differences Fig. 34. A plot of the correlation of STS and LiPFOS vs. SDS. The axes are deﬁned as
in methanol and acetonitrile as mobile phase modiﬁers. The pH the i/v LSER coefﬁcient ratio, where i = a, b, e, or s. STS vs. SDS (). LiPFOS vs. SDS of the solution has been held constant in all studies. Systems with the largest differences in their s-values represent those offering the Reprinted with permission from [97]. Copyright 2010 American Chemical Society.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 Table 8
Interpretations of energetic similarity or difference and thus selectivity similarity or different for various combinations of r2, slope, and intercept from correlations of LSER
coefﬁcient ratios from one system vs. those for another system.
Possible results for correlation of s/v, a/v, b/v, and e/v for two systems v1 = v2 Potentially effective = 1.00 or / Potentially effective = 1.00 or / = 0.00 or / Potentially effective and LiPFOS do not. Given the structural similarity of SDS to STS and separations that fail on one system may be better on the other. Or, the dissimilarity of SDS and LiPFOS, these results are not surprising.
the two systems together are candidates to be used as ‘orthogonal' Such plots are similar to Horvath et al.'s – plots [97,98] because systems in 2D separations. This, of course, assumes that the solute they fundamentally compare solute retention on one phase to that properties are such that they take advantage of the differences in on another. By using LSERs, though, the same compounds need not the energetics of retention. The elution order of n-alkanes is likely be run on each system as long as the solutes analyzed on each phase to be the same in all systems because there is only one dominant explore a wide range in type and strength of the intermolecular mode of interaction amongst them. To exploit system differences, interactions that govern retention. This makes many more system the solute set must differentially explore the interactions offered by the systems.
According to Horvath, two systems that yield a – plot with While the paragraph above focuses on ﬁnding chemically dif- a high correlation coefﬁcient and unity slope would be termed ferent systems, it is also important to point out the utility of the "homoenergetic" [98]. Linear regressions such as those shown in approach to ﬁnding comparable systems (those with high r2, unity Fig. 34 yield three statistical metrics: the slope, intercept, and cor- slopes, and v1 = v2). Such systems can be used as replacements to relation coefﬁcient of the ﬁt. We have shown [97] that for two yield comparable separations should such a need arise.
systems whose correlation yields slope = 1.00, intercept = 0.00, and As noted elsewhere [97] this approach uniﬁes three major con- r2 = 1.00, and whose v-coefﬁcients are equal, those systems will cepts in selectivity: (1) the general LSER formalism, or any other exhibit homoenergetic retention. This implies that the energetics multi-parameter model of retention such as the Snyder–Dolan of retention on both phases are identical and thus there is little to hydrophobic subtraction model, (2) Zhao and Carr's concept that no difference in their selectivities. In other words, there is no real the ratios of LSER coefﬁcients, not their absolute magnitudes, are chance for what Zhao and Carr called ‘effective selectivity' [81].
the important parameters for comparing system selectivity, and The two systems will yield the same order of elution and thus very (3) Horvath's – plots for classifying systems as homo-, homeo-, or heteroenergetic.
If the systems exhibit a high correlation and slope = 1.00, but the v-coefﬁcients for both LSERs are different such that v1/v2 / the situation would be termed ‘homeoenergetic', indicating a simi- 9.2. Visualizing the results using 3D plots lar physico-chemical basis for separation but no chances for elutionorder changes [98]. Again Zhao and Carr would say there is no real The above procedure requires that the LSER coefﬁcient ratios be chance for effective selectivity differences to exist between the two analyzed for each pair of systems of interest. For Fu and Khaledi's set systems [81]. It is possible that the solutes will be spread out on of 74 MEKC systems, this yields 2701 different comparisons that can one system more than the other, but the chance for fundamentally be performed. Performing the correlations is easily automated, but altering the separation does not exist.
understanding the output could be daunting if one tries to simply Finally, correlations between systems that yield slopes / look at the statistical output for this many correlations. A visual- intercepts / = 0.00 and/or low correlation coefﬁcients may exhibit ization method is needed. For that reason, we developed what we "heteroenergetic retention" [98]. In other words, retention on one call a system selectivity cube (SSC) – a three-dimensional plot for phase is not necessarily correlated with retention on the other.
which the axes are the slope, intercept, and correlation coefﬁcient Potential differences in selectivity exist between the two systems.
for system correlations. Every correlation of LSER coefﬁcient ratios In fact, elution order changes, and hence ‘effective selectivity dif- for two systems is then represented as a glyph in three-dimensional ferences' are possible. When two systems exhibit this kind of space. The name ‘system selectivity cube' is meant to recognize the relationship, if the desired separation is not being achieved with valuable contributions to chromatography arising from Snyder's one system then switching to the other system could improve the solvent selectivity triangle. The development and characteristics of the SSC are detailed elsewhere [97], but an example of the 3D Thus, correlating the LSER coefﬁcient ratios of one system vs.
plot based on the LSERs gathered by Fu and Khaledi is shown another and analyzing the slope, intercept, and correlation coef- ﬁcient can yield information about the similarity or differences We highlight here a few of the capabilities of this visualization in selectivity for the two systems. The possible combinations and their interpretations are shown in Table 8. The key point in Table 8is that retention on the two systems can be compared with three (1) The light green dot is a marker for the point with slope = 1.00, parameters: r2, slope, and intercept (a fourth dimension regarding intercept = 1.00, and r2 = 1.00 (in other words, highly correlated the relationship between v-coefﬁcients is needed to differentiate homo- and homeoenergetic retention). Speciﬁcally, systems with (2) The cube can be rotated, shrunk, or enlarged using a mouse to (1) non-unity slopes, (2) non-zero intercepts, or (3) poor correlation help highlight certain axes or certain regions of the cube. An coefﬁcients offer the possibility for ‘effective selectivity differences' example is shown in Fig. 36.
(i.e., elution order changes, dramatic changes in relative retention, (3) Different colors represent correlations between systems within etc.). In other words, their retention mechanisms are different and a group accordingto the groupings proposed by Fu and Khaledi Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 (A) Display only particular group correlations (e.g., correlations within group B).
(B) Display (or not) the maximum and minimum values on the (C) Change the maximum and minimum values for all of the axes.
The large grey ball at one corner indicates the minimum for allthree coordinates.
(D) Display (or not) the light green marker that represents highly correlated systems.
(E) Display the numeric coordinates of the points shown on the screen by hitting the ‘output' button. It is important to note herethat not only the slopes and intercepts are provided, but uncer-tainties in these values are also shown. Values of the correlationcoefﬁcients are also shown.
(F) Display only comparisons of interest by selecting individual systems (e.g., specify system 12 correlated with systems 19,22, 35, and 65).
(G) Add another dimension of data by displaying the v-coefﬁcient ratio for each comparison. Recall that when the v-coefﬁcients oftwo systems are equal, different energetics exist than when thev-coefﬁcients have different magnitudes. Thus, we have builtin an option to display ‘spikes' on the dots – the ‘spikier' the Fig. 35. Example of a 3D visualization made by plotting the slope, correlation coef-
dot, the larger the v-coefﬁcient ratio is for the two systems ﬁcient, and intercept resulting from the correlation of LSER coefﬁcient ratios for two represented by the glyph.
systems. Each point represents the regression results obtained by correlating two (H) A free version of the analysis and visualization software is avail- systems. Data from Fu and Khaledi's MST compilation was used to generate this plot. See text for other details. The correlation coefﬁcient axis goes from 0.00 (left)to 1.00 (right). The point representing an ideal homeoenergetic relationship has anr2 = 1.00, intercept = 0.00, and slope = 1.00. It is therefore on the rightmost face of the 9.3. Advantages of the system selectivity cube cube, roughly in the center and indicated with an arrow.
Reprinted with permission from [97]. Copyright 2010 American Chemical Society.
There are some signiﬁcant beneﬁts to the cube visualization compared to triangles: based on their selectivity triangle (blue = group A, red = groupB, green = group C, orange = group D).
• Basing the 3D comparisons on LSERs means that dozens, and (4) The pink glyphs represent comparisons between systems in sometimes hundreds of solutes have been used to generate the different groups.
coefﬁcients. This is likely more reliable than selecting only three (5) A user interface allows the user to representative solutes as was done in the early selectivity triangleschemes.
• Additionally, all of the LSER coefﬁcients are simultaneously con- sidered, unlike triangles which, even if based on LSERs, can onlyconsider three parameters at a time.
• As shown above for the Fu and Khaledi and Zhang and Carr reports, four separate plots are required to represent all of theparameters when using triangles. With the new approach, a sin-gle plot incorporates all of the data.
• Furthermore, if two systems are the same in three of the four LSER parameters, they will appear in the same group in one ofthe triangles and potentially in different groups in the other threetriangles. Here, if the fourth parameter is different enough toruin the correlation, the systems will immediately appear to bedifferent. See, for example, the plot for SDS vs. LiPFOS in Fig. 34.
• Unlike – plots which require the same solutes to be analyzed on both columns, with the LSER approach any representative setof solutes can be used to obtain the coefﬁcients upon which themethodology relies.
• Lastly, and perhaps most importantly, this approach can be applied to any multi-parameter model of retention – not justLSERs. For example, we have started analyzing the large RPLC dataset of Zhang and Carr discussed above which uses the hydropho-bic subtraction model to understand retention.
Fig. 36. Same plot as in the previous ﬁgure but rotated to make the correlation
9.4. Disadvantages of the system selectivity cube coefﬁcient axis more prominent. The default axes values are the high and low valuespresent in the data set but are not shown for clarity. The correlation coefﬁcient axesgoes from 0.00 (left) to 1.00 (right).
Some of the advantages of the new approach are also disad- Reprinted with permission from [97]. Copyright 2010 American Chemical Society.
vantages, depending on the analyst's goals.Here is a brief (and not Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 necessarily exhaustive) list of some of the important issues as we set, the two systems could provide nearly identical selectivities currently see them.
since the solutes cannot take advantage of the difference in thea/v ratios of the two systems. This could be mitigated with proper • LSER coefﬁcients generally have large relative uncertainties due weighting schemes, which we are considering. Ideally, the user to imperfections in the model. Thus, the slopes and intercepts of would get to input the weighting schemes and in this way get the correlations may be unreliable as a basis for ﬁrmly classify- to emphasize the solute characteristics they believe to be most ing similar and dissimilar systems. Nevertheless, we believe the approach can certainly serve as a helpful guide in distinguishingsystems.
Thus, much work remains to ﬁgure out how best to use this • Another disadvantage is the severe data reduction that is taking approach and to apply it to other data sets.
place and the chemical information that is lost in the process.
We introduced the SSC and the other methods for analyzing Hundreds of solutes are sometimes used to generate LSER equa- selectivity summarized earlier as alternatives and possible com- tions for a system. The LSERs themselves generally have ﬁve plements to or replacements for selectivity triangles. This brings or six ﬁtting parameters (therefore 10–12 values for two sys- us back full circle to the poem in our introduction. At some point, tems). Thus, in comparing two systems, hundreds of individual people stopped building pyramids, but as Jennifer Michael Hecht data points that relate directly to retention and selectivity, and urges "we must not curse the passage of time." up to a dozen LSER terms that also relate to solute retention,are getting simpliﬁed down to three or four parameters (slope,intercept, correlation coefﬁcient, and v-ratio). These four param- 10. Summary
eters are not immediately related to solute retention. Thus, alot of useful chemical information is not being used explicitly in Overall, we have traced the development of chromatographic this model. Such a process has an analogy in assigning semester selectivity triangle schemes over the past 50 years. Valid criticisms grades at most U.S. academic institutions. Throughout a semester, of some of the schemes were considered, and recent applications students take multiple tests and quizzes, write lab reports, turn based on new models of retention were highlighted. Finally, newer in homework, etc. – all of which contain very speciﬁc informa- methods for comparing system selectivity were presented.
tion about student performance. The scores on these individual Speciﬁcally, we started this review by examining the early ori- pieces get weighted and then averaged together to produce an gins of triangles as ﬁrst applied to GC stationary phases. We then overall semester average. This average is further simpliﬁed to focused largely on Snyder's original SST because it has received the a single semester grade on a ﬁve-grade scale of A through F.
most attention of all of the triangles produced. We discussed the So a lot of speciﬁc information is sacriﬁced for the simplicity of use of the SST in combination with simplex experimental designs obtaining a single letter grade. Likewise, our approach sacriﬁces to optimize LC separations. We have also discussed the complica- speciﬁc retention information for the sake of obtaining a simple tions that the presence of water in RPLC mobile phases causes when three-parameter comparison of system selectivity.
using selectivity triangles to make accurate predictions of selectiv- • Another concern that this approach shares with the triangles is ity. This stems from the effect that water has on the overall polarity the loss of chemical insight regarding the actual type and strength of the mobile phase, the speciﬁc changes it induces in the organic of intermolecular interactions governing separations. The glyph additives, and the speciﬁc polar and hydrogen bonding interactions merely tells the user if two systems are similar or different in it has with solutes. Because of these effects, even mobile phases of their energetics of retention but without any details regarding comparable solvent strength yield different selectivities. Because the speciﬁc blend of interactions. For this, an analysis of the LSERs the SST is based on pure solvents and does not incorporate the (or other model) would still need to be done.
effects of water, this generally limits the accuracy of predictions • As noted above, different amounts of water in RPLC mobile of RPLC selectivity that are based on the SST.
phases can have dramatically different effects on selectivity, and With regards to GC, many groups have used the SST approach the extent of those effects varies with the organic modiﬁer.
to characterize common stationary phase coatings. In the original As a result, the coefﬁcients of LSERs vary with percent water.
development of the SST, Snyder tried to remove the dispersion Thus, multiple LSERs would be required to fully characterize one effects by normalizing partition coefﬁcients of polar solutes to organic modiﬁer. The proposed selectivity cube could handle this those of hypothetical n-alkanes of comparable size. Furthermore, in terms of comparing one modiﬁer at one composition either to he based the SST apices on test solutes that do not explicitly repre- the same modiﬁer at a different composition or to a different sent dispersion interactions. In subsequent studies by other groups, modiﬁer at the same percent composition. In fact, any number of changing the test solutes was observed to change the location of the combinations of modiﬁer/composition could be compared, but phases within the triangle. The contributions of dispersion interac- the number of comparisons could be quite large and thus difﬁ- tions to selectivity were of speciﬁc interest in these studies, as well cult to fully evaluate. Furthermore, because of the different effects as some studies involving RPLC.
of water on different solvents, such comparisons will always be Fifteen years after the publication of Snyder's original SST, sol- system-speciﬁc and will not lead to general classiﬁcations regard- vatochromic parameters were used to show that the original Xe, ing the organic modiﬁers.
Xd, and Xn values represented blends of two or more intermolec- • Somewhat related to this, two systems may be poorly correlated ular interactions. In subsequent publications, a triangle based on because of a single parameter. For example, the a/v ratio could be solvatochromic solvent parameters was presented. This produced positive for one system and negative for another, with all other some advantages over the original version in terms of the chem- ratios generally the same. This is likely to still lead to a poor corre- ical interpretation of the triangle because of the relative ‘purity' lation and be interpreted as arising from two dissimilar systems.
of the parameters used to deﬁne the apices. Nevertheless, these Thus, differences in a single parameter may be overemphasized parameters cannot account for the effects of water on the nature in this approach (see again the correlation of SDS vs. LiPFOS in of the solvents. Thus, triangles based on solvatochromic parame- Fig. 34). This would be particularly important if the user's solute ters still suffer from the same complications regarding the practical set does not contain solutes that are hydrogen bond donating (i.e., application of triangles to predict RPLC selectivities.
no solutes with signiﬁcant A values). Our approach would lead More recently, selectivity triangles have been used in combi- one to believe that the systems are different, but for such a solute nation with LSERs to characterize pseudo phases used in MEKC Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 separations. The deﬁnition of the parameters, however, com- [2] R. Shepherd, R. Shepherd, 100 Symbols: What Shapes Mean in Art and Myth, plicates understanding their chemical meaning and potentially Thames and Hudson, London, 2002.
[3] L.S. Ettre, LC–GC North Am. 24 (2006) 680.
inﬂuences the groupings produced within the triangle. Using simi- [4] J. Michael Hecht, The Next Ancient World, Tupelo Press, North Adams, 2001.
larly deﬁned parameters, multiple triangles examining hundreds of [5] I. Brown, Nature 188 (1960) 1021.
commercially available RPLC phases have recently been published.
[6] I. Brown, J. Chromatogr. 10 (1963) 284.
[7] L.R. Snyder, J. Chromatogr. 92 (1974) 223.
These triangles, however, were based on the coefﬁcients produced [8] L. Rohrschneider, J. Chromatogr. 22 (1966) 6.
by the hydrophobic subtraction model of retention rather than on [9] W.T. Cooper, P.L. Smith, J. Chromatogr. 355 (1986) 57.
[10] L.R. Snyder, J. Chromatogr. Sci. 16 (1978) 223.
NPLC triangles were recently reviewed by Snyder. These trian- [11] L.R. Snyder, J.J. Kirkland, Introduction to Modern Liquid Chromatography, 2nd ed., Wiley–Interscience, New York, 1979.
gles emphasized the importance of solvent interactions with the [12] W.O. McReyolds, J. Chromatogr. Sci. 8 (1970) 685.
bare stationary phase – either through general non-localized or [13] W.O. McReynolds, Gas Chromatographic Retention Data, 5th ed., Preston Indus- speciﬁc localized interactions. Furthermore, the inﬂuence of sol- trial, Inc., Niles, IL, 1966.
[14] M.S. Klee, M.A. Kaiser, K.B. Laughlin, J. Chromatogr. 279 (1983) 681.
vent basicity on selectivity was also considered. Because of the [15] J.P. Teas, J. Paint Technol. 40 (1968) 19.
absence of water and its associated complications, predictions of [16] C.M. Hansen, J. Paint Technol. 39 (1967) 104.
selectivity based on NPLC triangles schemes are generally much [17] K. Nicolaus, C. Westphal (Eds.), The Restoration of Paintings, Konemann Ver- lagsgesellschaft mbH, Cologne, 1999, p. 360.
more accurate than those in RPLC.
[18] J. Wadum, Vermeer Illuminated: A Report on the Restoration of the View of Lastly, we closed this review by discussing other methods for Delft and The Girl with a Pearl Earring by Jonannes Vermeer, V+K Publish- comparing the selectivity of separation systems, focusing on our ing/Inmerc, Mauritshuis, The Hague, 1994, p. 22.
[19] J.L. Glajch, J.J. Kirkland, K.M. Squire, J.M. Minor, J. Chromatogr. 199 (1980) 57.
system selectivity cube. This work uniﬁes concepts that underpin [20] S.L. Morgan, S.N. Deming, J. Chromatogr. 112 (1975) 267.
selectivity triangles with theories regarding the homo-, homeo-, [21] M.W. Watson, P.W. Carr, Anal. Chem. 51 (1979) 1835.
and heteroenergetic nature of retention on two different systems.
[22] R.D. Snee, Chemtech 9 (1979) 702.
[23] S.R. Bakalyar, R. McIlwrick, E. Roggendorf, J. Chromatogr. 142 (1977) 353.
A 3D visualization method for simultaneously viewing hundreds [24] J.L. Glajch, J.J. Kirkland, Anal. Chem. 55 (1983) 319A.
or thousands of system comparisons was discussed. Potential [25] J.L. Glajch, J.J. Kirkland, L.R. Snyder, J. Chromatogr. 238 (1982) 269.
advantages and disadvantages of this new approach were brieﬂy [26] J.J. Kirkland, J.L. Glajch, J. Chromatogr. 255 (1983) 27.
[27] Sz. Nyiredy, B. Meier, C.A.J. Erdelmeier, O. Sticher, J. High Resolut. Chromatogr.
Chromatogr. Commun. 8 (1985) 186.
Given all of the advances that have occurred over the past half [28] G. D'Agostino, F. Mitchell, L. Castagnetta, M.J. O'Hare, J. Chromatogr. Biomed.
of a century in the development of selectivity triangles, it is natural Appl. 305 (1984) 13.
to end this review by turning to the future. The theory behind the [29] G. D'Agostino, L. Castagnetta, F. Mitchell, M.J. O'Hare, J. Chromatogr. Biomed.
Appl. 338 (1985) 1.
triangles seems to be well examined, and the advantages and dis- [30] W.J. Cheong, P.W. Carr, Anal. Chem. 60 (1988) 820.
advantages of various formulations are well understood. Perhaps it [31] J.H. Park, M.D. Jang, D.S. Kim, P.W. Carr, J. Chromatogr. 513 (1990) 107.
is time to shift the emphasis from creating more triangle schemes [32] E.B. Tada, L.P. Novaki, O.A. El Seoud, J. Phys. Org. Chem. 13 (2000) 679.
[33] Y. Marcus, Y. Migron, J. Phys. Chem. 95 (1991) 400.
to rigorously evaluating how well they do the job of characteriz- [34] A.M. Stalcup, D.E. Martire, S.A. Wise, J. Chromatogr. 442 (1988) 1.
ing selectivity that they are designed to do. We therefore suggest [35] E.D. Katz, K. Ogan, R.P.W. Scott, J. Chromatogr. 352 (1986) 67.
that it would be helpful to have studies aimed at using some of the [36] K.L. Rowlen, J.M. Harris, Anal. Chem. 63 (1991) 964.
[37] A. Alvarez-Zepeda, B.N. Barnum, D.E. Martire, Anal. Chem. 64 (1992) 1978.
recent publications involving MEKC and RPLC to show how selectiv- [38] I. Shulgen, E. Ruckenstein, J. Phys. Chem. B 103 (1999) 872.
ity triangles can be used to guide the selection of pseudo phases or [39] S.D. West, J. Chromatogr. Sci. 27 (1989) 2.
stationary phases for practical separations. In other words, perhaps [40] S.D. West, J. Chromatogr. Sci. 25 (1987) 122.
[41] J.J. Lewis, L.B. Rogers, R.E. Pauls, J. Chromatogr. 264 (1983) 339.
we need more examination of how reliably the triangles identify [42] L.C. Tan, P.W. Carr, J. Chromatogr. A 799 (1998) 1.
different and comparable phases for actual mixtures of interest, not [43] L.R. Snyder, P.W. Carr, S.C. Rutan, J. Chromatogr. A 656 (1993) 537.
just general test mixtures used to develop LSERs and the hydropho- [44] J.H. Hildebrand, R.L. Scott, The Solubility of Non-electrolytes, 3rd ed., Dover bic subtraction model. More speciﬁcally, perhaps such schemes can Publications, New York, 1964.
[45] B.L. Karger, L.R. Snyder, C. Eon, Anal. Chem. 50 (1978) 2126.
be shown to be effective for identifying orthogonal phases that can [46] E.F. Meyer, R.E. Wagner, J. Phys. Chem. 70 (1966) 3162.
be coupled in 2D RPLC separations. Relatedly, it is equally important [47] E.F. Meyer, T.A. Renner, K.S. Stec, J. Phys. Chem. 75 (1971) 642.
to be able to identify systems that have comparable selectivities [48] E.F. Meyer, K.S. Stec, R.D. Hotz, J. Phys. Chem. 77 (1973) 2140.
[49] E.F. Meyer, M.J. Awe, R.E. Wagner, J. Chem. Eng. Data 25 (1980) 371.
so that replacement systems can be readily adopted should some [50] B.R. Kersten, C.F. Poole, J. Chromatogr. 452 (1988) 191.
commercial phases become unavailable. Such studies, if successful, [51] C.F. Poole, S.K. Poole, Chem. Rev. 89 (1989) 377.
would then encourage the further development of fundamen- [52] P. Shah, H. Na, L.B. Rogers, J. Chromatogr. 329 (1985) 5.
[53] T.J. Betts, J. Chromatogr. 354 (1986) 1.
tal triangles schemes for characterizing, selecting, and optimizing [54] S.T. Preston, J. Chromatogr. Sci. 8 (1970) 18A.
separation systems.
[55] W.T. Cooper, L.Y. Lin, Chromatographia 21 (1986) 335.
[56] R.M. Smith, Anal. Chem. 56 (1984) 256.
[57] S.C. Rutan, P.W. Carr, W.J. Cheong, J.H. Park, L.R. Snyder, J. Chromatogr. 463 [58] M.J. Kamlet, J.L. Abboud, R.W. Taft, J. Am. Chem. Soc. 99 (1977) 6027.
[59] M.J. Kamlet, R.W. Taft, J. Am. Chem. Soc. 98 (1976) 377.
We thank Dr. Lloyd Snyder and Professor Peter Carr for their [60] R.W. Taft, M.J. Kamlet, J. Am. Chem. Soc. 98 (1976) 2886.
helpful comments and discussions throughout the preparation of [61] M.J. Kamlet, J.L.M. Abboud, M.H. Abraham, R.W. Taft, J. Org. Chem. 48 (1983) this manuscript. We also thank the reviewers for their helpful [62] M.J. Kamlet, T.N. Hall, J. Boykin, R.W. Taft, J. Org. Chem. 44 (1979) 2599.
suggestions and detailed consideration of this review. Acknowl- [63] R.W. Taft, J.L.M. Abboud, M.J. Kamlet, J. Am. Chem. Soc. 103 (1981) 1080.
edgment is made to the Donors of the American Chemical Society [64] J.H. Park, A.J. Dallas, P. Chau, P.W. Carr, J. Phys. Org. Chem. 7 (1994) 757.
[65] M.F. Vitha, J. Chem. Educ. 78 (2001) 370.
Petroleum Research Fund for partial support of this research.
[66] E.H. Slaats, W. Markovski, J. Fekete, H. Poppe, J. Chromatogr. 207 (1981) 299.
Support was also provided by the Drake University Science [67] R.M. McCormick, B.L. Karger, Anal. Chem. 52 (1980) 2249.
Collaborative Institute (DUSCI).
[68] R.M. McCormick, B.L. Karger, J. Chromatogr. 199 (1980) 259.
[69] C.R. Yonker, T.A. Zweir, M.F. Burke, J. Chromatogr. 241 (1982) 257.
[70] C.R. Yonker, T.A. Zwier, M.F. Burke, J. Chromatogr. 241 (1982) 269.
[71] R.P.W. Scott, P. Kucera, J. Chromatogr. 142 (1977) 213.
[72] C.S. Koch, F. Köster, G.H. Findenegg, J. Chromatogr. 406 (1987) 257.
[73] A. Tilly-Melin, Y. Askemark, K.G. Wahlund, G. Schill, Anal. Chem. 51 (1979) 976.
[1] J. Tresider (Ed.), The Complete Dictionary of Symbols, Chronicle Books, San [74] D.E. Martire, R.E. Boehm, J. Phys. Chem. 87 (1983) 1045.
Francisco, 2004.
[75] M.R. Böhmer, L.K. Koopal, R. Tijssen, J. Phys. Chem. 95 (1991) 6285.
Author's personal copy
A.R. Johnson, M.F. Vitha / J. Chromatogr. A 1218 (2011) 556–586 [76] J. Li, Y. Zhang, P.W. Carr, Anal. Chem. 64 (1992) 210.
[88] L.R. Snyder, J. Planar Chromatogr. 21 (2008) 315.
[77] J. Li, Y. Zhang, A.J. Dallas, P.W. Carr, J. Chromatogr. 550 (1991) 101.
[89] L.R. Snyder, J.L. Glajch, J.J. Kirkland, J. Chromatogr. 218 (1981) 299.
[78] J. Li, Y. Zhang, H. Ouyang, P.W. Carr, J. Am. Chem. Soc. 114 (1992) 9813.
[90] Y. Ishihama, N. Asakawa, J. Pharm. Sci. 88 (1999) 1305.
[79] B.R. Kersten, S.F. Poole, C.F. Poole, J. Chromatogr. 468 (1989) 235.
[91] M.H. Abraham, F. Martins, J. Pharm. Sci. 93 (2004) 1508.
[80] J. Li, A.J. Dallas, P.W. Carr, J. Chromatogr. 517 (1990) 103.
[92] E. Lázaro, C. Ràfols, M.H. Abraham, M. Rosés, J. Med. Chem. 49 (2006) 4861.
[81] J. Zhao, P.W. Carr, Anal. Chem. 71 (1999) 2623.
[93] E. Fuguet, C. Ràfols, E. Bosch, M.H. Abraham, M. Rosés, Electrophoresis 27 (2006) [82] C. Fu, M.G. Khaledi, J. Chromatogr. A 1216 (2009) 1891.
[83] C. Fu, M.G. Khaledi, J. Chromatogr. A 1216 (2009) 1901.
[94] M.R. Euerby, P. Petersson, J. Chromatogr. A 994 (2003) 13.
[84] M.H. Abraham, A. Ibrahim, A.M. Zissimos, J. Chromatogr. A 1037 (2004) [95] U. Neue, K.J. Fountain, P.C. Iraneta, B.A. Alden, K. Wyndham, Pittcon 2010, Orlando, FL, paper no. 2890-2, March 4, 2010.
[85] M.F. Vitha, P.W. Carr, J. Chromatogr. A 1126 (2006) 143.
[96] L.R. Snyder, J.W. Dolan, P.W. Carr, R.E. Majors, LC–GC 28 (2010) 418.
[86] Y. Zhang, P.W. Carr, J. Chromatogr. A 1216 (2009) 6685.
[97] A.R. Johnson, M.F. Vitha, T. Urness, T. Marrinan, Anal. Chem. 82 (2010) 6251.
[87] L.R. Snyder, J.W. Dolan, P.W. Carr, J. Chromatogr. A 1060 (2004) 77.
[98] W. Melander, J. Stoveken, C. Horvath, J. Chromatogr. 199 (1980) 35.

Source: http://craiguniversity.tk/media/departmentsoffices/dusci/pdfdocuments/Chromatography-selectivity-triangles.pdf

Tai chi and postural stability in patients with parkinson's disease

Tai Chi and Postural Stability in Patients with Parkinson's Disease Fuzhong Li, Ph.D., Peter Harmer, Ph.D., M.P.H., Kathleen Fitzgerald, M.D., Elizabeth Eckstrom, M.D., M.P.H., Ronald Stock, M.D., Johnny Galver, P.T., Gianni Maddalozzo, Ph.D., and Sara S. Batya, M.D. BACKGROUNDPatients with Parkinson's disease have substantially impaired balance, leading to di- From the Oregon Research Institute (F.L.),

Boletín de infraestructuras de burgos

[Boletín de Infraestructuras de Burgos] [Cuarto trimestre 2011] Boletín de Infraestructuras de Burgos [ASOCIACIÓN PLAN ESTRATÉGICO DE BURGOS] [En este número] Ha pasado un año desde la publicación del último boletín. En este tiempo, la situación económica del país no ha permitido grandes novedades en el estado de la construcción de nuevas infraestructuras, salvo en la apertura