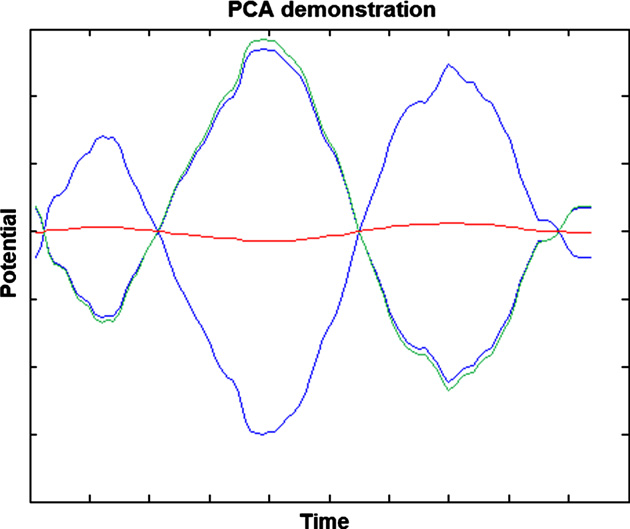
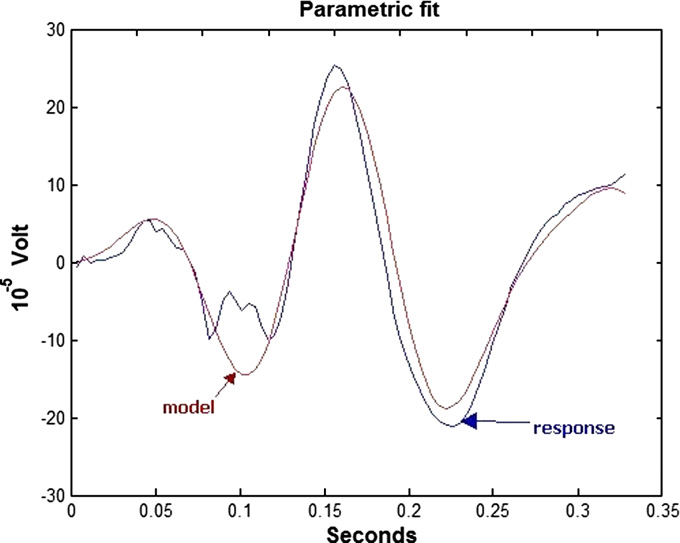
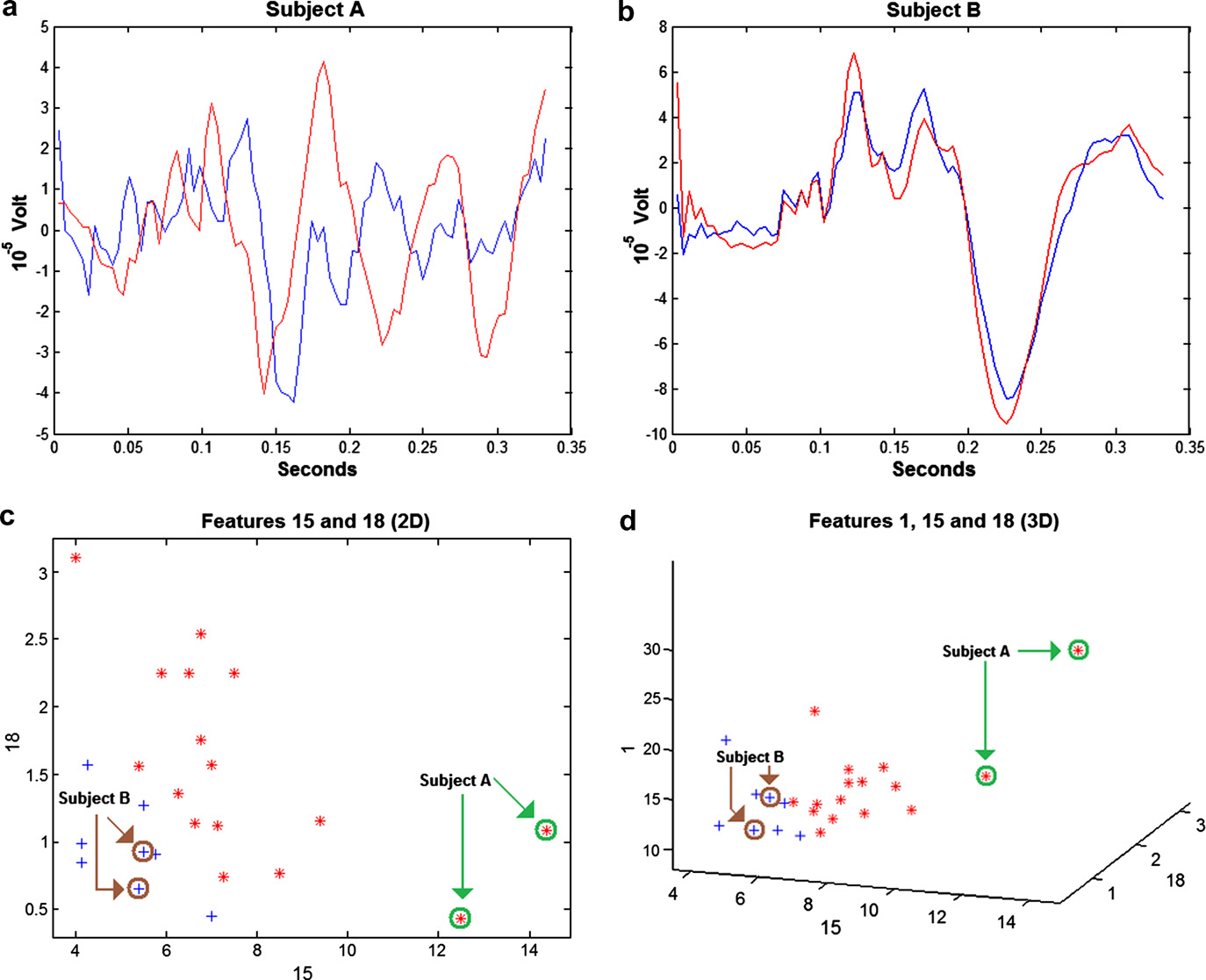
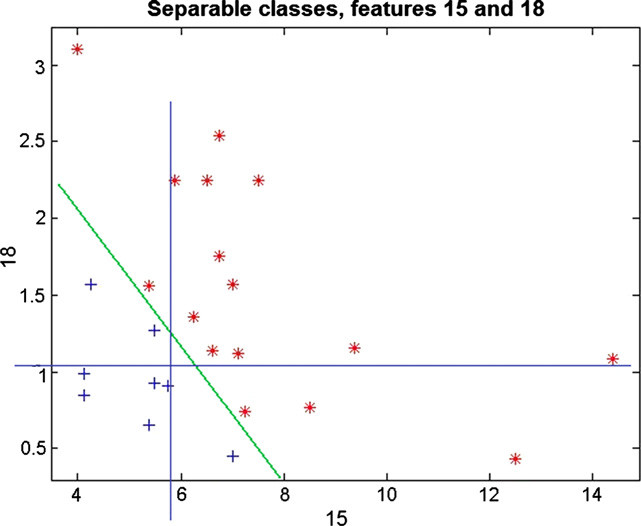
lqs.li
Fragen RID: 1) Welches Regelwerk gilt für die grenzüberschreitende Beförderung gefährlicher Güter mit Eisenbahnen? a) RID b) ADR c) VTGGS d) ADNR e) IMDG-Code 2) Welches Regelwerk gilt für die grenzüberschreitende Beförderung gefährlicher Güter mit Eisenbahnen? 3) In welchem Regelwerk finden Sie Aussagen zur allgemeine Sicherheitsvorsorge